Lesson Coordinates and the Cartesian Plane

Learning Objectives

After this lesson, students should be able to:

• Describe the Cartesian plane and correctly label its parts.
• Explain the source of the name "Cartesian."
• Describe the naming convention for coordinates in the form (x, y).
• Explain what a function is and how to tell if a set of coordinates is a function.
• Determine the domain and range of a set of points.
• Plot a set of data points.
• Explain how understanding graphing will help with solving the challenge.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

Worksheets and Attachments

Pre-Req Knowledge

Familiarity with the coordinate plane, coordinates and equations are helpful but not required.

Introduction/Motivation

(In advance, make copies of the Work It Out Worksheet.Then prepare to shows students the 11-slide Linear Functions Presentation PowerPoint® file, which provides notes for them. The presentation is composed of three sections, delineated by three different slide background colors [blue, gray, gold]. The slides are "animated," so click the mouse [or space bar] to make the next items appear. Show slides 1-4 with the Introduction/Motivation section. Show slides 4-8 when presenting the Lesson Background information. Use slides 9-11 in conjunction with the associated activity, Club Function; they are included in this lesson presentation as a teacher preview of the activity.)

(While showing slides 1-4, present the following information to students.)

Have you ever liked two things so much that you wanted to combine them to make one amazing thing? (Listen to student comments.) For example, think about peanuts and chocolate chips. Combined together, they can make peanut butter cookies with chocolate chips on top! Or what about the game of Slamball? It combines the fun of jumping on a trampoline with the rules of basketball. Both great ideas, and there are many more.

One interesting combination has to do with a French man who really liked math back in the 1600s. His name was Rene Descartes, and he liked both algebra and geometry, but back then people did not think those two topics were very much related. Decartes started looking for ways to combine them so that they could be used together for important applications. He came up with this neat way of taking numbers that belong in the realm of algebra and plotting them visually onto a geometric coordinate plane to show how they are related. This coordinate plane became known as the "Cartesian plane," named after him.

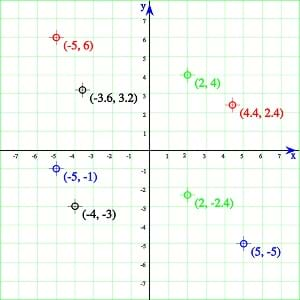
Several parts of the coordinate plane are important to understand before we can learn how to use it. In today's lesson, you will learn about it and how it is used.

(Hand out the worksheets and continue on to present students with the Lesson Background content.)

Lesson Background and Concepts for Teachers

While still showing slide 4 of the attached PPT file, cover the following information with students, as they make notes on the worksheet:

• Take students through labeling the axes with "x" and "y," as well as adding arrows to the ends of each axis to show it goes on forever.
• Talk about the Cartesian plane quadrants, having students label them "I, II, III and IV."
• Point out which directions are positive (right on the x-axis and up on the y-axis) and which directions are negative (left on the x-axis and down on the y-axis), and have students mark out scales on each axis.
• Point out the origin, the point (0,0).

While still showing slide 4, begin talking about coordinates: What does (0,0) mean? Students may say moving to 0 units to the left or right on the x-axis and moving 0 units up or down on the y-axis. Prompt them further to tell you which is x and which is y. Then tell them that we can generally write the format as (x,y), and have them fill that in on their worksheets.

Go through the process of plotting a couple of points with them. Depending on their level of familiarity with the topic, little prompting may be necessary. When they understand the concept, have them practice plotting the coordinates on the bottom of their worksheets. Then review the answers as a class and clarify any misconceptions. (This is a good stopping place for shorter class periods, as students can finish plotting points as homework.)

While showing slides 5 – 8, teach students the definition of a function. Use the slides to define relations, functions, domain, range, and linear functions. Have students do the practice problems on slide 8 and discuss their answers as a class.

For homework, assign students to complete the worksheet (if not done in class) and the Lesson 2 Practice Sheet Homework on the coordinate plane, function, domain and range.

Note: Slides 9 – 11 explain the Club Function game activity rules (only included here for teacher preview). Refer to the associated Club Function activity for detail and examples.

Associated Activities

• Club Function - Students learn about relations and functions through an interactive modeling game.

Assessment

Practice: During the lesson (or as homework), have students complete the Work It Out Worksheet to practice plotting some coordinates on their own.

Journal Questions: At lesson end, have students create in their journals small graphs of the data points from the grand challenge data set. Graph the first 10 points. Create the appropriate scale and approximate the location of each point. Then have them write answers to the following questions.

1. Do you see a trend forming?
2. Draw a line approximating this trend.
3. What did this graph tell you that you did not already know from looking at the data?
4. Why is graphing a set of data important?
5. Where do you think this data could have come from?

Homework: Assign students to complete the Lesson 2 Practice Sheet Homework on coordinate plane, functions, domain and range to give them practice determining whether a group of points is a function, and determining the domain and range of sets of points.

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.