Lesson Graphing Equations on the Cartesian Plane:
Slope

Learning Objectives

After this lesson, students should be able to:

• Define slope as the ratio of vertical rise to horizontal run.
• Determine the slope of a line given a graph.
• Determine the slope of a line given two points on the line.
• State the formula for slope as:

  

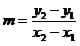
• Compare slopes of graphs in terms of "more steep," "less steep," etc.
• State what types of lines have slopes of zero or undefined and why.
• Compare slopes of parallel and perpendicular lines.
• Explain how understanding slope will help solve the grand challenge for this unit.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

Worksheets and Attachments

Pre-Req Knowledge

Students must know how to graph points on the Cartesian plane. They must be familiar with the x- and y- axes on the plane in the positive and negative directions.

Introduction/Motivation

Let's return to the grand challenge, which asked us to analyze a data set. Can anyone suggest what exactly "analyze" means in this context? (Possible answers: To find trends, model data, predict future data.) Today, we will explore one way of graphically depicting data points. It remains your challenge to apply what you learn today toward solving the grand challenge.

Earlier, we talked about how to graph points on the Cartesian plane. Today, we want to begin graphing lines on the coordinate plane. In order to do this, you must know about a characteristic of the line called slope. The slope is a numerical value that tells us how slanted the line is, and it can help us distinguish one line from another.

Lesson Background and Concepts for Teachers

The slope of a line is given the variable "m," and it is equivalent to the vertical rise over the horizontal run of a line. For example, one might wish to determine the slope of a line between the points (0,3) and (6,5). One way to get this is to graph the points, as discussed in our previous lesson, and count how far up and over you have to go to get from one point to the other. On this sense, slope can be defined as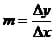

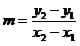
The slope between the sample points (0,3) and (6,5) is positive because it is increasing from left to right. Show students other examples of positive slopes or have them suggest examples. Tell them that a line can also have negative slope, and ask them to draw one either on paper or on individual dry erase boards and hold it up for you to see. After determining that they have drawn a line with negative slope, ask them what the slope of their lines would be. Remind them that it's usually best to pick two points that are whole numbers to avoid estimation, when possible.

Give students the following example: A ladder rests against a wall such that the top touches at (0,16) and the bottom at (10, 0). What is the slope of the ladder? (The answer is -8/5. Remind students that you must reduce a fraction.)

Next, ask students to graph the line containing the point (1,2) and having a slope of m=3/4. They should be able to plot the point and count the slope from that point to the next point.

Finally, draw a horizontal line on a coordinate plane and ask students to determine its slope. In doing so, they should pick out two points, plug in the formula, and notice that the numerator simplifies to zero. A horizontal line has m=0. Then have them repeat the exercise with a vertical line such that they find that they must divide by zero to get the slope. Tell students this is why we say that vertical lines have undefined slope. Relate this to skiing so they have a way to remember which is which. Tell them that a slope of zero is okay because you would not be moving anywhere, but an undefined slope would be really bad because it would be a fall straight down.

The last part of this lesson focuses on parallel and perpendicular lines. Write the following table on the classroom board and ask students whether they think the two lines will ever intersect based on the solutions listed. To confirm their responses, graph the points on a coordinate plane so everyone can see that the two lines are parallel. Make the relationship clear that parallel lines have the same slope.

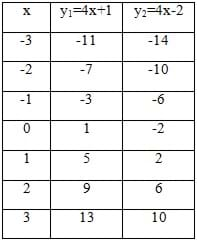
Then ask students what the slope of a line that is perpendicular to the two lines above that has a slope of 4 would be. What do they think the slopes of perpendicular lines would be? Lead them to the idea that the slopes are exact opposites, or negative reciprocals of one another. If the slope of a line was 4, then a perpendicular line would have a slope of -1/4. Ask students if a line had a slope of 1/6, what the slope of a perpendicular line be? (It would be -6.) Point out that perpendicular lines form right angles with one another and intersect at exactly one place.

Wrap up the lesson by relating it back to the challenge question. Ask students to get out the sheets of paper or journals where they have been recording ideas. Tell them to write down how this information on slope might help them solve the challenge question.

Lesson Closure

Let's finish up by returning to our grand challenge. Open your journals to your initial thoughts and responses generated a few days ago. Now add some notes about what we've learned over the past two lessons. How will plotting data points and graphing lines play a role in analyzing the data you've been provided? In addition, do you have any additional thoughts of possible data sources?

Assessment

Post-Lesson Assessment: Homework on Slope: Students practice a variety of problems involving the slope of lines. They complete the problems as homework and bring them back the next day to self-assess their understanding and correct any mistakes.

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.