Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Lesson Dependency:
Subject Areas: Algebra
Summary
Students learn about four forms of equations: direct variation, slope-intercept form, standard form and point-slope form. They graph and complete problem sets for each, converting from one form of equation to another, and learning the benefits and uses of each.Engineering Connection
The idea of slope as the rate of change is essential to understanding how lines are graphed. Engineers must be able to create and also understand graphs that can explain sets of data. Mechanical engineers read and understand graphs that show displacement, velocity and acceleration to then analyze data from testing sites to learn how to design their products (such as cars and airplanes) to be more efficient and safe. In journal questions 5-6 of the summary assessment, students think as engineers, considering the meaning of key data points and the purpose of using lines to model data.
Learning Objectives
After this lesson, students should be able to:
- Distinguish between different forms of equations, including direct variation, slope-intercept form, standard form and point-slope form.
- Explain what is meant by the term equivalent equations.
- Convert from one form of equation to another.
- Tell when each form is useful and how to graph using each form.
- Use the slope of a parallel or perpendicular line along with a point on the line to write the equation of the line in any of the three main forms.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin.
(Grade
7)
More Details
Do you agree with this alignment?
-
Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane; derive the equation y = mx for a line through the origin and the equation y = mx + b for a line intercepting the vertical axis at b.
(Grade
8)
More Details
Do you agree with this alignment?
-
Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
(Grade
8)
More Details
Do you agree with this alignment?
-
Describe qualitatively the functional relationship between two quantities by analyzing a graph (e.g., where the function is increasing or decreasing, linear or nonlinear). Sketch a graph that exhibits the qualitative features of a function that has been described verbally.
(Grade
8)
More Details
Do you agree with this alignment?
-
Solve linear equations in one variable.
(Grade
8)
More Details
Do you agree with this alignment?
-
Analyze and solve pairs of simultaneous linear equations.
(Grade
8)
More Details
Do you agree with this alignment?
-
Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Create equations in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Create equations and inequalities in one variable and use them to solve problems. Include equations arising from linear and quadratic functions, and simple rational and exponential functions.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Use devices to control technological systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
National Council of Teachers of Mathematics - Math
-
Use mathematical models to represent and understand quantitative relationships
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/van_linear_eqn_less4] to print or download.Pre-Req Knowledge
Students must understand that linear equations have other equivalent forms that may be determined just by rearranging the equation using properties of equality. They must also know how to graph points on a coordinate plane and determine the slope of a line. Prior knowledge of intercepts is also recommended.
Introduction/Motivation
Last time we met, you learned about an important characteristic of linear functions – their slopes. Today and in the next few class periods, we will be putting that knowledge to good use by looking at different ways we can write the equations of a line. It is important to realize that a line's equation can take an infinite number of forms, but people use a few forms more often than others because they are useful to indicate slope and other characteristics of the line. These characteristics of the line can represent important components of data, as will be seen in the associated activity on motion.
Lesson Background and Concepts for Teachers
Begin by bringing back the line from last class that passed between the points (0,3) and (6,5). Remind students that they determined this slope to be 1/3. However, it would be nice to recognize this line beyond just its slope. What would really be great is to create a relationship between the two variables x and y. Remind students that for any given linear function, every value of x has exactly one corresponding y value. For a different linear function, that x value may have a different corresponding y-value. So part of what we need to do is characterize the line such that we give a relationship between x and y, no matter what the numerical values are for that function.
One "special case" that is interesting to start with is the relationship of variables that have direct variation with one another. That is, they follow the relationship y = k x , where k is the "constant of variation." This is seen in the relationship between distance, speed, and time, where speed is held constant as y and x vary directly from one another. Because students are widely familiar with the relationship between speed, distance, and time, have them do a hands-on activity to demonstrate this relationship (see below for the Matching the Motion activity). These relationships found in the activity are important for engineers when analyzing data. For example, mechanical engineers must understand the different relationships between speed, distance and time in order to best and and safely design products such as cars and airplanes. For now, students should know how to determine the constant of variation (which is the slope of the line), given a pair of values (x, y). They also need to know how to determine one value given the other value and the constant of variation. For example, "y varies directly as x. y=4 when x=0.5. What is k? Write an equation. When y=2, what is x?" Sample work is shown below.
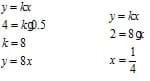
The direct variation relationship is really just a special case of the next form of equations students will look at, slope-intercept form. The only difference is that it always has a y-intercept of 0 (crosses at the origin).
The first widely accepted form of an equation is slope-intercept form. For this form, we need to know – you guessed it – the slope of the line and its y-intercept. (The y-intercept is where the line crosses the y-axis.) Slope intercept equations take the following form: y = m x + b , where m is the slope and b is the y-intercept. So if you know the slope of the line, as discussed in our previous lesson, and you know where it crosses the y-axis (the y-intercept), then you can write the equation of the line. For example, y=2x+3 has a slope of 2 and crosses the y-axis at positive 3. Students should be able to take an equation in any other form and convert it to slope-intercept form by re-arranging the equation using properties of equality. An example is shown below.
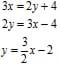
Students should also be able to move easily between algebraic and graphical representations of the linear relationship.
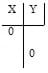
The second important form of equations is standard form, which is written as Ax + By = C. Students should know that, unlike slope-intercept form, it is more difficult to obtain this form directly from the graph because A, B and C are not the slope, intercepts or any other characteristic of the line. The best way to write this type of equation from a graphed line is to find the line in another form, like slope-intercept form, and then re-arrange the equation so that it is in standard form. he beauty of the standard form of an equation is that one can easily determine x- and y-intercepts from it and use these points to graph. To do this, encourage students to make an x-y table as shown below. Plug in 0 for x and see what y is. Then plug in 0 for y and see what x is. With these two points, students can easily make a graph of the linear function. Students should also be able to convert an equation into standard form.
The third form equation students should know about is point-slope form of a line, which is 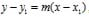
Wrap up the lessons by relating them back to the challenge question. Ask students to get out their sheets of paper or journals where they have been recording ideas. Tell them to write down how this information on forms of equations might help them solve the challenge question.
For homework each night, have students complete the attached worksheets.Provide them with the Forms of Lines handout to study with.
Associated Activities
- Matching the Motion - Students learn about slope, determining slope, distance vs. time graphs through a motion filled activity.
Assessment
Lesson Summary Assessment:
- Returning to the data provided in the grand challenge, what information can you immediately determine from the data?
- Can you fill out the following chart?

- What is the benefit of using each slope form?
- Would any form be more appropriate for the data provided in the grand challenge?
- Think of a possible source of the grand challenge data. Now, what do the intercepts tell you about that type of data?
- What is the purpose of using a line to model data?
Homework:
- Homework on Direct Variation: Students practice finding the constant of variation and determining one variable given the other variable and the constant of variation. Have them complete and bring back in the next day to self-assess their understanding and correct their mistakes.
- Homework on Slope-Intercept Form: Students practice a variety of problems with slope-intercept form, including graphing. Have them complete and bring back in the next day to self-assess their understanding and correct their mistakes.
- Homework on Standard Form: Students practice graphing from standard form and converting to and from standard form. Have them complete and bring back in the next day to self-assess their understanding and correct their mistakes.
- Homework on Point-Slope Form: Students practice graphing from point-slope form and converting to and from point-slope form. Have them complete and bring back in the next day to self-assess their understanding and correct their mistakes.
- (optional) Summative Assessment Over All Forms: Assign students to create posters or "cheat sheets" explaining why each form is useful and how to graph using each form.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn how to quickly and efficiently interpret graphs, which are used for everyday purposes as well as engineering analysis. The focus is on students becoming able to clearly describe linear relationships by using the language of slope and the rate of change between variables.

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

Students learn about linear programming (also called linear optimization) to solve engineering design problems. They apply this information to solve two practice engineering design problems related to optimizing materials and cost by graphing inequalities, determining coordinates and equations from ...
Copyright
© 2013 by Regents of the University of Colorado; original © 2007 Vanderbilt UniversityContributors
Aubrey McKelveySupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: June 7, 2019









User Comments & Tips