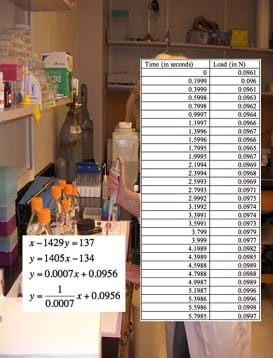
Summary
Prepared with pre-algebra or algebra 1 classes in mind, this module leads students through the process of graphing data and finding a line of best fit while exploring the characteristics of linear equations in algebraic and graphic formats. Then, these topics are connected to real-world experiences in which people use linear functions. During the module, students use these scientific concepts to solve the following hypothetical challenge: You are a new researcher in a lab, and your boss has just given you your first task to analyze a set of data. It being your first assignment, you ask an undergraduate student working in your lab to help you figure it out. She responds that you must determine what the data represents and then find an equation that models the data. You believe that you will be able to determine what the data represents on your own, but you ask for further help modeling the data. In response, she says she is not completely sure how to do it, but gives a list of equations that may fit the data. This module is built around the legacy cycle, a format that incorporates educational research findings on how people best learn.Engineering Connection
The most important engineering concepts are based around linear functions. It is necessary to understand graphing points and lines, slope and different forms of equations that make up linear equations. As part of their jobs, engineers often interpret data and determine lines of best fit for given data sets. The engineering applications that are useful can be represented in a variety of ways. Particularly of interest is direct variation, which is the form many engineering applications take, including Hooke's law and Ohm's law. When considering slope though, engineers must be able to read and understand graphs that show displacement, velocity and acceleration to then analyze data from testing sites to learn how to design their products to be more efficient and more safe. Other engineers use Ohm's law frequently for it states the most basic relationship between voltage, current and resistance. It is used in almost all calculations to analyze and test circuits in any electrical piece or equipment or device.
Unit Overview
The design uses a contextually based "Challenge" followed by a sequence of instruction in which students first offer initial predictions ("Generate Ideas") and then gather information from multiple sources ("Multiple Perspectives"). This is followed by "Research and Revise" as students integrate and extend their knowledge through a variety of learning activities. The cycle concludes with formative ("Test Your Mettle") and summative ("Go Public") assessments that lead student towards answering the Challenge question. The progression of the legacy cycle through the unit is described below.
The research and ideas behind this way of learning may be found in How People Learn: Brain, Mind, Experience, and School: Expanded Edition (Bransford, Brown & Cocking, National Research Council. Washington, DC: The National Academies Press, 2000; read entire text at https://www.nap.edu/catalog.php?record_id=9853).
The legacy cycle is similar to the engineering design process in that they both involve identifying needs existing in society, combining science and math to develop solutions, and using research conclusions to design a clearly conceived solution to the original challenge. The engineering design process and the legacy cycle both result in correct and accurate solutions, with an empahsis on how the solution is devised and presented. See an overview of the engineering design process at https://en.wikipedia.org/wiki/Engineering_design_process.
In lesson 1, students are presented with the following grand challenge: You are a new researcher in a lab, and your boss has just given you your first task to analyze a set of data. It being your first assignment, you ask an undergraduate student working in your lab to help you figure it out. She responds that you must determine what the data represents and then find an equation that models the data. On your own, you must decide the source of the data, and the undergraduate student helps with the modeling by providing a list of equations that may fit. It is your job to decide which, if any, will help analyze the data.
Students begin by Generating Ideas in a journal and answering questions, such as: What does this table of values mean? Do you have any initial ideas on what to do with the data? What do you need to know more about? and What do you already know that is relevant? Then students are asked to consider the perspective of an electrical engineer as part of the Multiple Perspectives step of the legacy cycle.
In lesson 2, students enter the Research and Revise step focusing on how to plot coordinates on a Cartesian plane. They also learn how to distinguish a relation as a function through a fun-filled activity.
Lesson 3 returns students to the Research and Revise step for further learning. This lesson includes teacher instruction on slope and parallel vs. perpendicular lines.
Lesson 4 proceeds in the Research and Revise phase, but introduces the concepts of different forms of equations for lines, and the benefits and uses of each form. These forms include direct variation, slope-intercept form, standard form, and point-slope form. Many of these and previous concepts are demonstrated in an activity involving a Vernier motion detector.
Lesson 5 concludes the Research and Revise phase of the legacy cycle by presenting applications of different linear functions including speed, Hooke's law and Ohm's law. An end of unit test covers all the material learned and represents the Test Your Mettle phase. Finally, students Go Public by creating documents that presenttheir solutions to the challenge question, demonstrating their knowledge of the material and problem solving skills.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
See individual lessons and activities for standards alignment.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!Unit Schedule
- Day 1: The Challenge Question lesson
- Day 2: Coordinates and the Cartesian Plane lesson
- Day 3: Club Function activity
- Day 4-5: Graphing Equations on the Cartesian Plane: Slope lesson
- Day 6: Forms of Linear Equations lesson
- Day 7: Matching the Motion activity
- Day 8: Applications of Linear Functions lesson
- Day 9: Can You Resist This? activity
- Day 10: Spring Away! activity
More Curriculum Like This

Students are introduced to the "Walk the Line" challenge question. They write journal responses to the question and brainstorm what information they need to answer the question.

Students are introduced to Hooke's law as well as stress-strain relationships. Through the lesson's two-part associated activity, students 1) explore Hooke's law by experimentally determining an unknown spring constant, and then 2) apply what they've learned to create a strain graph depicting a tumo...
Assessment
- End-of-Unit Test (attached to Lesson 5)
- Lesson 5 includes the final Go Public phase of the legacy cycle in which students apply the concepts they have learned to answer the Grand Challenge question. They prepare one-page documents outlining how they found their lines of best fit with the given data.
Copyright
© 2013 by Regents of the University of Colorado; original © 2007 Vanderbilt UniversityContributors
Aubrey MckelveySupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: January 17, 2018




User Comments & Tips