Lesson The Challenge Question

Learning Objectives

After this lesson, students should be able to:

• Explain the challenge problem.
• List what information might be needed to answer the problem.
• Group together similar areas of knowledge needed for the challenge.
• Explain how engineers apply linear equations to the engineering problem solving process.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

Introduction/Motivation

Challenge Question: You are a new researcher in a lab, and your boss has just given you your first task to analyze this set of data: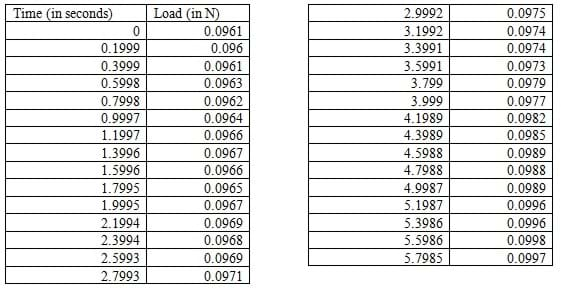

Since it is your first work assignment, you ask an undergraduate student working in your lab to help you figure it out. She says that you must determine what the data represents and then find an equation that models the data. You believe that you will be able to determine what the data represents on your own, but you ask for further help modeling the data. In response, she says she is not completely sure how to do it, but that one of the following equations might be useful: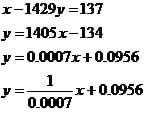

Which, if any, of these equations helps you analyze the data? How does it help? Why did you choose that equation?

Lesson Background and Concepts for Teachers

This lesson covers the Challenge, Generate Ideas, and Multiple Perspectives perspectives phases of the legacy cycle. The aim is to get students to brainstorm ideas and organize their information. Begin with students working alone to record their personal thoughts and ideas on the problem, including what they already know (or think they know) and what they think they might need to know. Then, after an adequate amount of time (5-10 minutes), have students share and suggest ideas and record on the classroom board the knowledge areas students identify. Organize the suggestions using a concept map.

Then, read the following interview with an engineer (below) and give students time to brainstorm additional ideas of needed information. After they are satisfied with their list of information needed, guide them into breaking down the challenge question into four knowledge areas: graphing points on a coordinate plane, graphing an equation on a coordinate plane, different forms of equations, and application.

"As an engineer, the first thing I wonder is what the data shows us. I can see that the load increases as time increases. This shows me that the load is being added to as time goes by. This is similar to the energy used in an office building in the morning as people come into work. As time passes, more people come in and the energy being used increases. I also notice that this data seems to be increasing at a constant rate or, as a mathematician would say, linearly. This would be like a person coming into the office every five minutes and turning on his or her light. At five minute intervals, the energy used for lights would increase by one light's worth of power. To model this increase we could use a linear equation to graph a straight line, which shows how the energy increases over time. In our case, the load increase also seems to be linear. A computer might be useful for telling us if the data is truly linear. In our research, we could use an equation to give us a better idea of what will happen to the load at different points in time. This would help us understand the process we are researching."

– Brad McKelvey, electrical engineer

Assessment

After Challenge Journal Topics:

• What might this data represent, why?
• Do you have any initial ideas on what to do with the data?
• What do you need to know more about?
• What do you already know that is relevant?

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.