Quick Look
Grade Level: 12 (11-12)
Time Required: 5 hours 45 minutes
(seven 50-minute sessions)
Expendable Cost/Group: US $5.00 This activity also uses some non-expendable (usable) items; see the Materials List for details.
Group Size: 3
Activity Dependency:
Subject Areas: Algebra, Measurement, Physics, Problem Solving
NGSS Performance Expectations:

| HS-ETS1-2 |
| HS-ETS1-3 |
| HS-PS3-3 |
Summary
Students apply high school-level differential calculus and physics to the design of two-dimensional roller coasters in which the friction force is considered, as explained in the associated lesson. In a challenge the mirrors real-world engineering, the designed roller coaster paths must be made from at least five differentiable functions that are put together such that the resulting piecewise curving path is differentiable at all points. Once designed mathematically, teams build and test small-sized prototype models of the exact designs using foam pipe wrap insulation as the roller coaster track channel with marbles as the ride carts. Project constraints students must consider include: initial cart velocity of zero (at the highest point), and final path end velocity of zero. The design must be efficient enough that the initial potential energy of the body is sufficient for it to complete the entire path. To achieve an efficient design, students use a formula obtained in the associated lesson—one that gives the velocity of a spherical body rolling on a curved path when friction is present. This equation considers the body’s energy lost due to friction, and is used to estimate the maximum height the marble may reach after rolling from a hill. Students use Excel® to make these calculations and graph the designed path and velocities. To conclude, teams summarize their procedures, designs, results, and theory-vs.-reality experiences in a slide or video presentation to their classmates, including their small-scale physical models. This activity and its associated lesson are designed for AP Calculus. A pre-quiz, PowerPoint® presentation, spreadsheet calculations/graphs (with and without calculus), and student instructions/grading rubric are provided.
Engineering Connection
With their breathtaking elevation changes and speeds, spine-chilling roller coasters rides are the star attractions of amusement parks. All the various up, down and around designs all work because of gravity, inertia and friction. In this activity, by designing a simple roller coaster, students consider the same forces that professional engineers do when designing rides. Students apply mathematics, energy conservation principles and computation software to completely define the path and optimal dimensions for their designs. Then they use simple materials to build and test functional roller coaster models, which gives them the opportunity to address prototype construction problems and the unanticipated details that impact the expected design performance. Also like professional engineers, students find solutions to these problems.
Learning Objectives
After this activity, students should be able to:
- Create a design given certain requirements and constraints.
- Create, using parabolas, a piecewise differentiable function given specific vertices and determining tangency points.
- Estimate the velocity of a rolling body along a curved path, considering friction forces.
- Use computational software (such as Excel®) to evaluate and graph functions.
- Build a functional model from a mathematically generated design.
- Determine the possible causes why physical models might not behave exactly as expected in the theoretical, mathematically derived, “on-paper” design.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-2. Design a solution to a complex real-world problem by breaking it down into smaller, more manageable problems that can be solved through engineering. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Design a solution to a complex real-world problem, based on scientific knowledge, student-generated sources of evidence, prioritized criteria, and tradeoff considerations. Alignment agreement: | Criteria may need to be broken down into simpler ones that can be approached systematically, and decisions about the priority of certain criteria over others (trade-offs) may be needed. Alignment agreement: | |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-3. Evaluate a solution to a complex real-world problem based on prioritized criteria and trade-offs that account for a range of constraints, including cost, safety, reliability, and aesthetics, as well as possible social, cultural, and environmental impacts. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Evaluate a solution to a complex real-world problem, based on scientific knowledge, student-generated sources of evidence, prioritized criteria, and tradeoff considerations. Alignment agreement: | When evaluating solutions it is important to take into account a range of constraints including cost, safety, reliability and aesthetics and to consider social, cultural and environmental impacts. Alignment agreement: | New technologies can have deep impacts on society and the environment, including some that were not anticipated. Analysis of costs and benefits is a critical aspect of decisions about technology. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS3-3. Design, build, and refine a device that works within given constraints to convert one form of energy into another form of energy. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Design, evaluate, and/or refine a solution to a complex real-world problem, based on scientific knowledge, student-generated sources of evidence, prioritized criteria, and tradeoff considerations. Alignment agreement: | At the macroscopic scale, energy manifests itself in multiple ways, such as in motion, sound, light, and thermal energy. Alignment agreement: Although energy cannot be destroyed, it can be converted to less useful forms—for example, to thermal energy in the surrounding environment.Alignment agreement: Criteria and constraints also include satisfying any requirements set by society, such as taking issues of risk mitigation into account, and they should be quantified to the extent possible and stated in such a way that one can tell if a given design meets them.Alignment agreement: | Energy cannot be created or destroyed—it only moves between one place and another place, between objects and/or fields, or between systems. Alignment agreement: Modern civilization depends on major technological systems. Engineers continuously modify these technological systems by applying scientific knowledge and engineering design practices to increase benefits while decreasing costs and risks.Alignment agreement: |
Common Core State Standards - Math
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Create equations and inequalities in one variable and use them to solve problems. Include equations arising from linear and quadratic functions, and simple rational and exponential functions.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve a simple system consisting of a linear equation and a quadratic equation in two variables algebraically and graphically.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve equations and inequalities in one variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Fit a function to the data; use functions fitted to data to solve problems in the context of the data.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Analyze functions using different representations
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Build a function that models a relationship between two quantities
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of engineering design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the attributes of design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Design problems are seldom presented in a clearly defined form.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
The design needs to be continually checked and critiqued, and the ideas of the design must be redefined and improved.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Engineering design is influenced by personal characteristics, such as creativity, resourcefulness, and the ability to visualize and think abstractly.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
A prototype is a working model used to test a design concept by making actual observations and necessary adjustments.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use computers and calculators to access, retrieve, organize, process, maintain, interpret, and evaluate data and information in order to communicate.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Illustrate principles, elements, and factors of design.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Document trade-offs in the technology and engineering design process to produce the optimal design.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Determine the best approach by evaluating the purpose of the design.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use various approaches to communicate processes and procedures for using, maintaining, and assessing technological products and systems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Texas - Math
-
apply mathematics to problems arising in everyday life, society, and the workplace;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
use a problem-solving model that incorporates analyzing given information, formulating a plan or strategy, determining a solution, justifying the solution, and evaluating the problem-solving process and the reasonableness of the solution;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate, and techniques, including mental math, estimation, and number sense as appropriate, to solve problems;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriate;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
display, explain, or justify mathematical ideas and arguments using precise mathematical language in written or oral communication.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Functions. The student uses process standards in mathematics to explore, describe, and analyze the attributes of functions. The student makes connections between multiple representations of functions and algebraically constructs new functions. The student analyzes and uses functions to model real-world problems. The student is expected to:
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
graph exponential, logarithmic, rational, polynomial, power, trigonometric, inverse trigonometric, and piecewise defined functions, including step functions;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
graph functions, including exponential, logarithmic, sine, cosine, rational, polynomial, and power functions and their transformations, including af(x), f(x) + d, f(x - c), f(bx) for specific values of a, b, c, and d, in mathematical and real-world problems;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
determine and analyze the key features of exponential, logarithmic, rational, polynomial, power, trigonometric, inverse trigonometric, and piecewise defined functions, including step functions such as domain, range, symmetry, relative maximum, relative minimum, zeros, asymptotes, and intervals over which the function is increasing or decreasing;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
analyze situations modeled by functions, including exponential, logarithmic, rational, polynomial, and power functions, to solve real-world problems;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Texas - Science
-
demonstrate common forms of potential energy, including gravitational, elastic, and chemical, such as a ball on an inclined plane, springs, and batteries;
(Grades
9 -
10)
More Details
Do you agree with this alignment?
-
investigate examples of kinetic and potential energy and their transformations;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
describe the transformational process between work, potential energy, and kinetic energy (work-energy theorem);
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
The student describes the nature of forces in the physical world. The student is expected to:
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- polyethylene pipe wrap insulation, such as Armacell Tubolit half-inch x 6-ft length for ~$1 from Home Depot; although foam pipe insulation material that is larger than the half-inch size can be used as the coaster rails/channel, the half-inch size is more flexible
- vinyl bullnose archway corner bead, such as Clark Western ¾-in x 10-ft length from Home Depot for ~$4, which will be cut into approximately one-inch segments; alternatively, use some other material/way to provide L-bracket-type support to attach the curving half-pipe insulation rail to a cardboard backing
- 1 corrugated cardboard or plastic sheet, 3 x 4-ft size works well; note; large pieces of cardboard can be scavenged from large bicycle and appliance boxes; alternatively, have students tape together smaller cardboard pieces (see Figure 13)
- a few glass marbles, half-inch diameter; make sure the marble diameter is less than the internal diameter of the pipe insulation so the rolling marbles have only one contact point with the insulation surface
- masking tape (1-inch thick) and super glue, for adhering pipe insulation to itself and to cardboard/plastic backing
- scissors and/or utility knife, for cutting pipe insulation and vinyl corner bead
- yardstick or 1-meter ruler with inch-scale markings
- computer with Microsoft® Excel® and PowerPoint®, or similar software applications
- Project Rubric, one per group
- A Frictional Roller Coaster Pre-Quiz, one per person
- (optional) 2 x 4-foot pegboard with one-inch-apart drilled holes, used as a mat to make it easier to graph/draw points on the cardboard backing
To share with the entire class:
- projector and computer to show the class the A Frictional Roller Coaster Presentation, a PowerPoint® file, including some online videos
- kitchen scale, or other small scale capable of measuring the mass of a marble in grams
- (optional) capability to take photographs and/or videos of the roller coaster models in use
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/ind-1996-frictional-roller-coaster-design-project-calculus] to print or download.Pre-Req Knowledge
- Conic sections, parabolas
- Microsoft® Excel® formulas and graphs
- Microsoft® PowerPoint®
- Solving non-linear systems of equations
- Piecewise functions
- Continuous functions
- Differential calculus and derivatives
- Differentiable piecewise functions
- Concepts and equations presented in the associated lesson: A Tale of Friction
Introduction/Motivation
(Be ready to show the 17-slide A Frictional Roller Coaster Presentation, a PowerPoint® file, including some online videos. The slides are animated, so a mouse or keyboard click brings up the next text, image and/or slide.)
(Slides 1-2) Does anyone have any idea of the cost of roller coaster projects? (Play some of the three short videos linked in slide 2 about roller coaster construction and computer modeling.)
(Slides 3-5) Do you have any idea of the cost of projects like these? Guess the cost for each of these three roller coasters (also shown in Figure 2). (Write students’ guesses on the board. Then tell them the answers.) El Toro cost ~$25 million, Thunder Dolphin cost ~$37 million, and Millennium Force cost ~$25 million. (How close were they in their cost estimations?) Disney’s Expedition Everest ride at Walt Disney World in Florida is the most expensive roller coaster, costing $100 million and taking more than six years to create.
For projects that cost so much—like these world-class roller coasters—the designs and construction are complex and challenging tasks for engineers.
(Slide 7) Have you ever worked on a roller coaster project? (Expect students to answer yes. If so, ask them to briefly describe what they did. Expect that some students may have used a marble as a cart and a flexible material to construct the roller coaster path. They placed an initial point very high and then created a path with hills, valleys and the most loops possible. Then they tested the path and if the marble stopped or flew away, they modified the path until the marble was able to complete the entire path. Next, if desired, play some of the nine videos linked on slide 7 to show some student roller coaster school projects.)
Great, I’m sure you really had fun working on those projects. Do you think engineers do the same? I mean, do you think they build a complex structure, then test and modify the path sections where the cart gets stuck or flies off? (Expect students to say something like, “no, that does not sound like a reasonable process since they would have to demolish parts of the built structure and build again.”)
You are right. That approach would be terribly inefficient. To make real-world structures, engineers first create an efficient design that takes into consideration all the conditions and factors that may affect performance. They often create virtual simulations of the coaster in action (as you saw in two of the videos). One of the many factors engineers must consider is friction. In your school roller coaster projects, you were aware that friction was an important factor. You saw how the marbles never reached a height equal to their initial drop heights and every time the marble achieved a lower height. While you understood that this happened because of friction, you were unable to estimate its effect.
In today’s activity, you will work in teams like professional engineers who work on those expensive multi-million-dollar projects from the design to the final product. This is your design challenge:
- Design a simple roller coaster, that is, one with two dimensions—only hills and valleys—but consider friction forces from the beginning of the design process. Define the path by a function so that every point on the path is precisely defined with an (x, y) pair. Precisely determine the maximum possible height of every hill such that the marble is able to complete the entire path, moved only by its potential energy at the initial point of the path. The initial velocity is zero and the final velocity must be zero, or practically zero.
- Build and test a prototype using a marble as the cart, pipe insulation for the coaster’s path and a large cardboard sheet to hold the model track. Your prototype dimensions must match those in your design, and like the roller coasters created by professional engineers, your prototype must behave as expected in your design. No major changes in the path or dimensions are permitted. If you run into problems, you will determine why your prototype is not performing as expected.
Procedure
Background
Typical middle and high school roller coaster projects do not quantify the friction force present. For students in these grade bands, it is explained that roller coasters work because potential energy transforms into kinetic energy and vice versa, and that the initial potential energy builds up the kinetic energy to propel a cart through the remainder of the ride. It is also explained that the work done by friction forces is what eventually stops the cart, but no quantification is provided for this work along the coaster’s path. At most, the overall work done by friction is estimated by computing the kinetic-potential energy losses using the work-energy theorem (R1).
In the high school AP Physics C course, students solve some problems involving friction, using the work-energy theorem. They may find the velocity of a body sliding on a flat surface while considering the friction present. So high school students are able to understand the solution of a spherical body rolling along a curved path, with friction being considered.
In the associated lesson, A Tale of Friction, it is explained in detail using high school differential calculus and physics how to find a formula to determine the velocity of a sphere rolling along a simple roller coaster path considering friction (1):
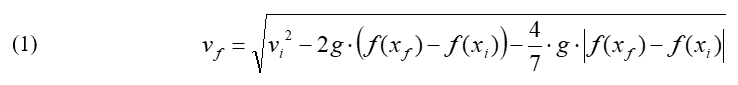
Equation (1) is the magic key to successfully design a functional simple roller coaster with its path defined by a function f (x). Because it is not easy to find a single function describing a roller coaster’s path, f (x) must be defined as a differentiable piecewise function (see Figure 1). Depending on the time available for this activity, and your students’ math and physics background, decide what portions of the lesson to teach to your students, so that at the end they understand equation (1), and how to use it to test whether their designs will work or not.
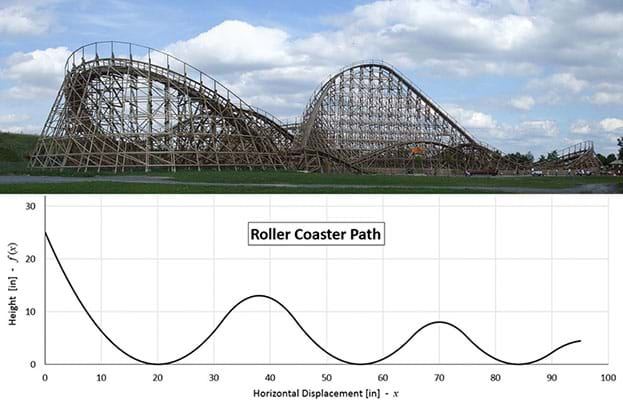
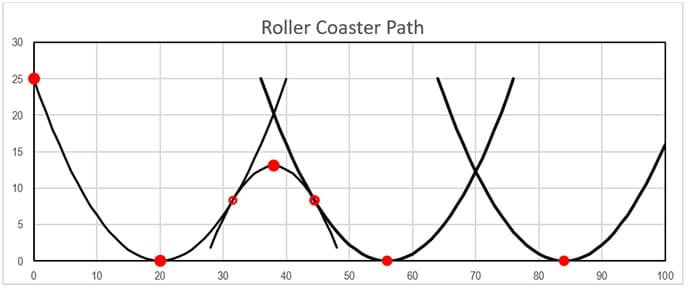
In this activity, students design a Russian Mountain path using upward-opening and downward-opening parabolas. With parabolas, it is relatively simple to create a differentiable piecewise function. They are easy to define, given the vertex and a point on the graph.
As in any engineering project, constraints and conditions must be considered in the design. The roller coasters will be fabricated from polyethylene pipe wrap insulation, use a rolling marble as the cart, and be attached to a flat surface. Our roller coaster curves must resemble those of real Russian Mountains (Figure 2) and the slopes must not be very steep because the marbles may slide instead of roll.

A roller coaster’s initial height and slope determines its length. The higher the initial point, the longer the path. It is best that the initial roller coaster slope not be steeper than ±2.5, otherwise the marble may slide instead of roll. This guideline is an outcome from testing different initial slopes.
It is recommended that inches be used for the measurements and calculations because all construction and auxiliary materials are measured in inches. Following are the details for the design and construction of a roller coaster.
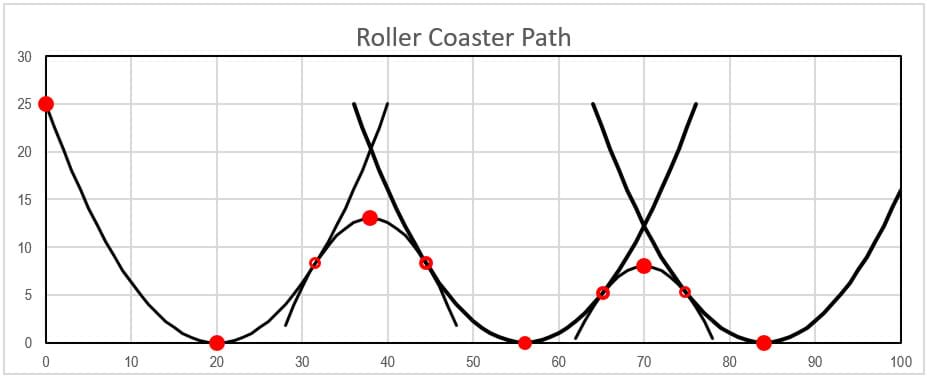
The design begins by defining the initial (highest) roller coaster point (x0, y0) and the slope of the parabola at that spot. This highest point is on the left branch of the first upward-opening parabola (see Figure 3). To simplify calculations, place the initial point on the y-axis, and the vertices of the upward-opening parabolas on the x-axis. This example describes an initial point 25 inches above the x-axis: (x0, y0) = (0, 25), and a slope of ±2.5 at this point. With this initial data, the vertex of the first upward-opening parabola (h, k) = (h1, 0) can be determined.
Because the parabola vertex is involved in these calculations, the vertex form equation is used:


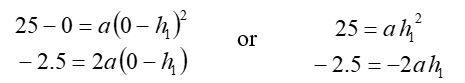
Solving this system, we find that:
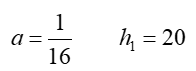
The equation for the first parabola is then:

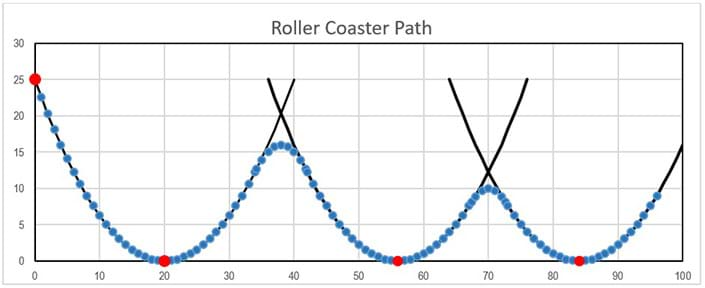
The next two upward-opening parabolas may be placed more or less arbitrarily. Remember to place their vertices at the same level as the parabola 1 vertex, but not too close to each other since the closer the vertices, the steeper the path of the parabolas joining them will be, and the marble is more inclined to slide instead of roll if the path is too steep. Because a parabola is symmetric with respect to its vertical axis, it is convenient if all three upward parabolas have the same width (see Figure 3); this choice simplifies the involved calculations very much.
In this example (Figure 3), the next vertices are (h3, k3) = (56, 0) and (h5, k5) = (84, 0). These three upward-opening parabolas join smoothly with three downward-opening parabolas. The heights of the vertices of the downward-opening parabolas must be such that the marble passes that hill with a very low velocity but enough to continue rolling to the next hill and past it and so on. It is expected that the marble stops (or almost stops) at the end of the designed path. These heights cannot be set up arbitrarily; the friction along the path must be considered. If we roll a marble along a single U-path, we know that friction stops the marble before it reaches a height equal to the initial height. Therefore, equation (1) must be applied in every upward-opening parabola to estimate the height the marble may reach at the end of that portion of the path. Once that height is determined, the vertex for the downward-opening parabolas may be defined, and the next step is to join them smoothly with the upward-opening parabolas.
For the parabola with vertex (h3, k3) = (56, 0) and same width as (3), the corresponding equation is:

and for the parabola with vertex (h5, k5) = (84, 0), the corresponding equation is:

The x-coordinate of the vertices of the downward-opening parabolas is at the middle of the x-coordinates of the vertices of the upward-opening parabolas (see Figure 5). Determine the height of these vertices using equation (1):
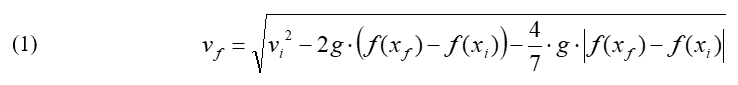

f (0) = 25
vi =v (0) = 0
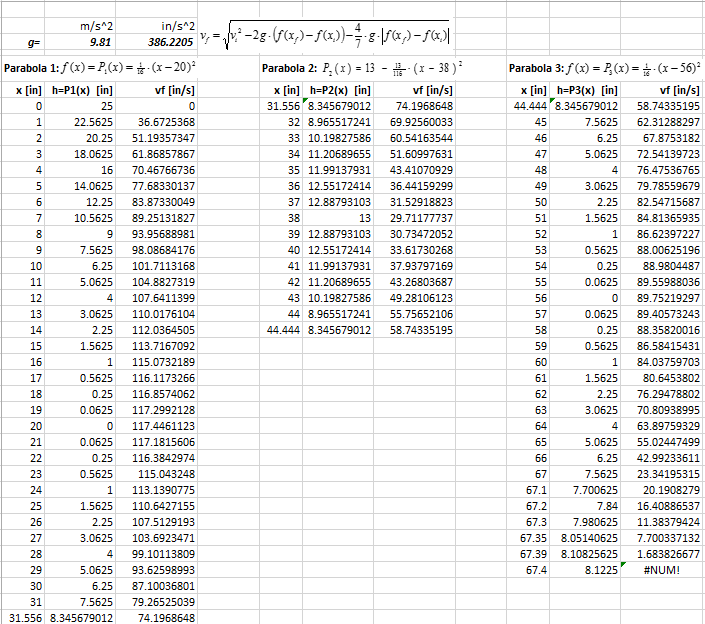
Now it is necessary to evaluate equation (1) along the parabolic path (3). For this purpose, the path is divided into little straight sections and on every section a final velocity is computed, taking as initial velocity the final velocity computed for the previous section. These calculations can be easily performed in Excel® (see Figure 4). (Note: Expect students to create their own spreadsheets, guided by the teacher.)
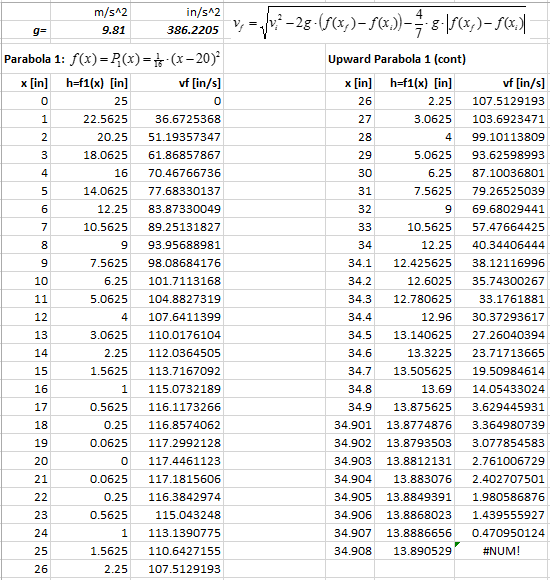
The previous computations show that the marble will stop at a point with horizontal distance from the origin between 34.907 and 34.908 inches, reaching a height of no more than 13.89 inches. It is reasonable to place the vertex of the second parabola at about 13 inches high.
Placing the vertex of parabola 2 (see Figure 5) at the middle of the parabolas 1 and 3 vertices, (h2, k2) = (38, 13), the equation for parabola 2 is:
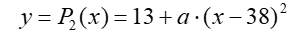
To find the value of coefficient a, the condition that parabolas 1 and 2 must be tangent to each other (Figure 5), must be solved. This condition is expressed as two equations:
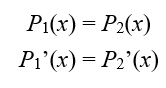
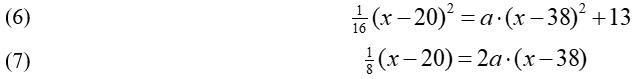
From (7), substituting in (6):
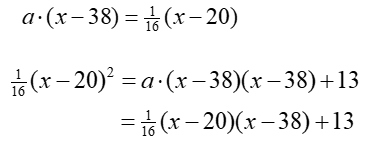
Grouping and solving for x:
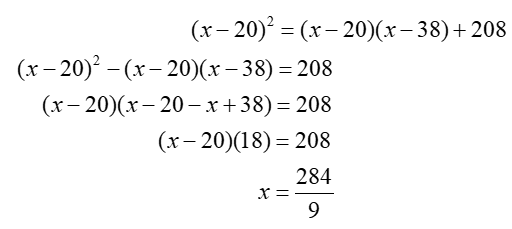
Substituting this value in (7), and solving for a:
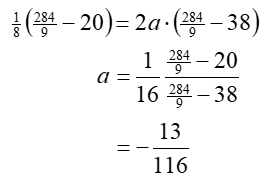
The equation for parabola 2 is then:
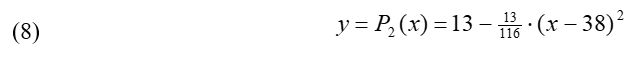
Using equation (8), we find the y-coordinate of the tangency point:
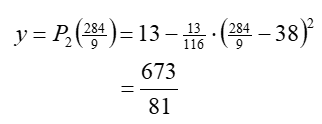
Because of symmetry, (8) is also tangent to parabola 3. This second tangency point is at the same horizontal distance from the parabola 2 vertex, but to the right, and of course, at the same height (Figure 5):
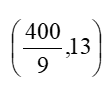
The first two branches of the roller coaster path are completely defined:
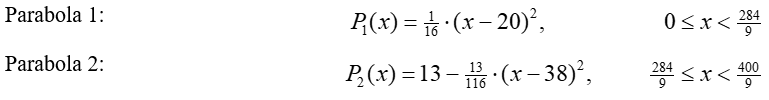
To find the equation of the second downward-opening parabola (Figure 6), repeat the above procedure. Equation (5) must be used beginning at x0 = 0 again to estimate the height the marble may reach at the end of parabola 3. Once this height is determined, the parabola 4 vertex can be defined, and its equation determined solving the tangency condition with parabola 3.
Using Excel® again (Figure 7):
From these computations, it is reasonable to place the vertex of the fourth parabola at about 8-inches high. Again, placing this vertex between the parabolas 3 and 5 vertices, (h4, k4) = (70, 8), the equation for parabola 4 is:
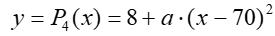
Again applying the tangency condition to parabolas 3 and 4:
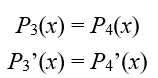
Or
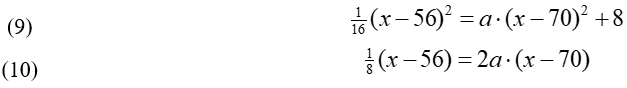
and solving equations (9) and (10), the value of the constant a and the tangency point coordinates is determined:
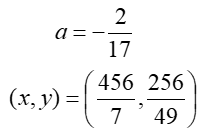
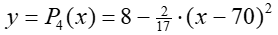
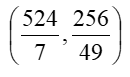
The next two branches of the roller coaster path are now completely defined:
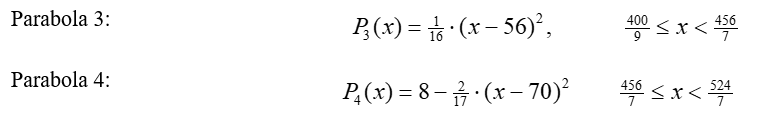
The last two parabolas need to be determined in the same way. Analyzing the velocities along the parabolas 1 to 5 (Figure 8):
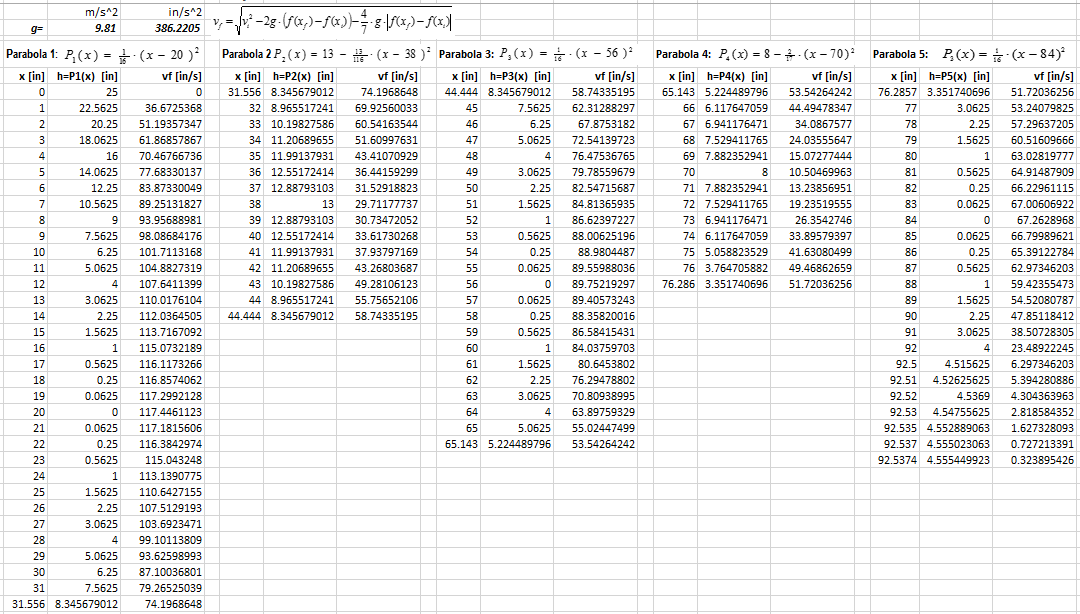
The maximum height predicted for parabola 5 is 4.5555 inches. The vertex of parabola 6 is placed at (h6, k6) = (96, 4.5) where the marble is expected to stop (or almost stop). The proposed equation for this parabola is then:
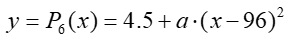
Applying again the tangency condition to parabolas 5 and 6:
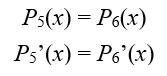
Or
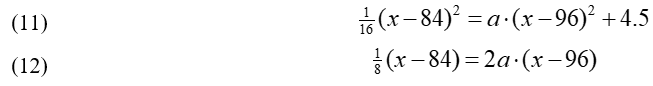
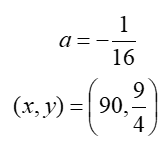
The equation for parabola 6 is then:
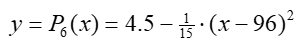
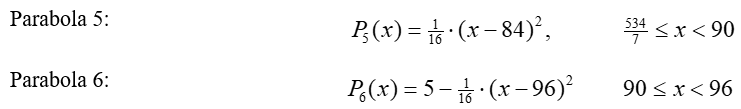
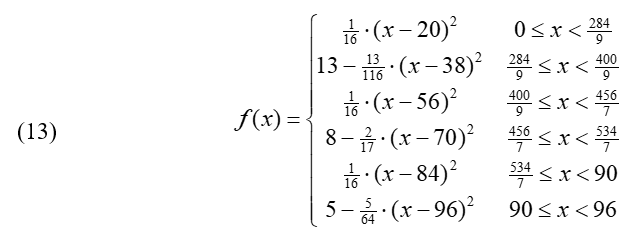
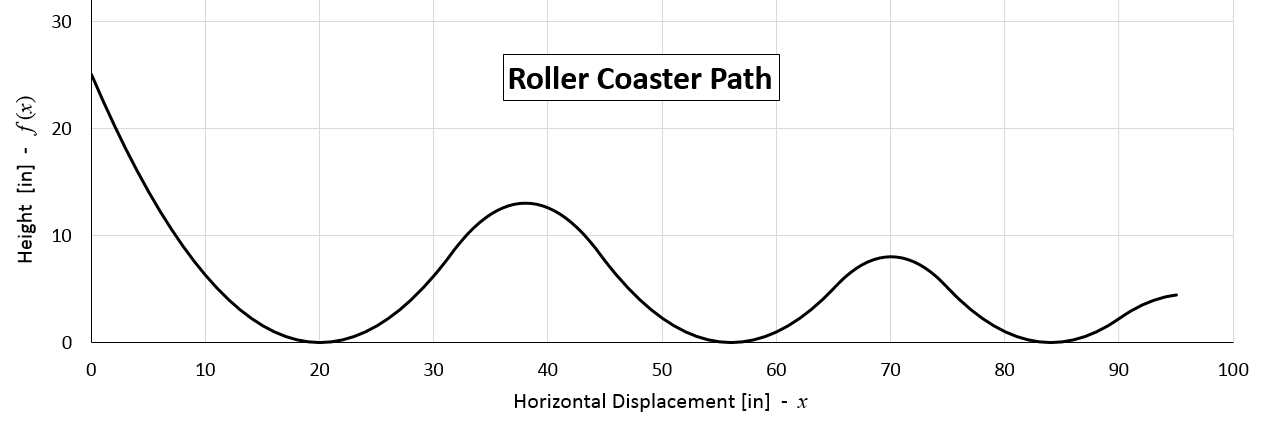
Figure 10 shows the graph of the predicted velocities along the path of this design:
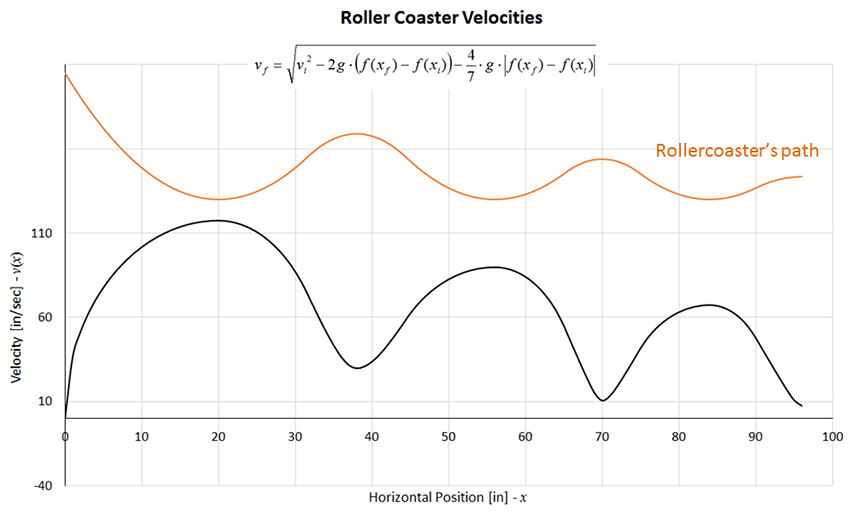
At this point, a natural question is: How did friction behave along the path? Friction was considered in order to predict the above velocities and to design the roller coaster path, but until now, friction has not been explicit. To answer this question, it is necessary to evaluate the equations obtained in the associated lesson that correspond to the static friction coefficient and the friction force for the rolling marble:

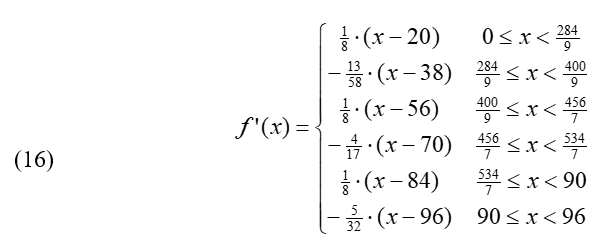
To express the friction force in Newtons (N), it is necessary to change the units used until now, inches, into meters (1 m = 39.37 inches). So, the derivative of our piecewise function in meters is:
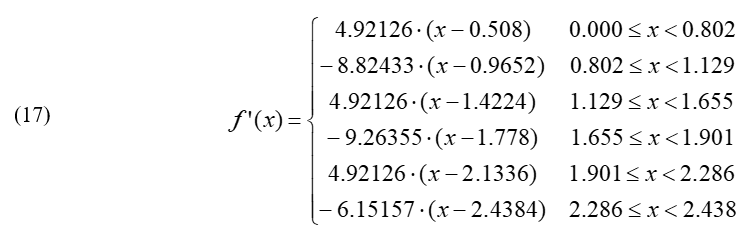
Taking g = 9.81 m/s, and a marble mass m = 0.004 kg, again use Excel® (Figure 11) to evaluate the coefficient of friction μs and the friction force fs.
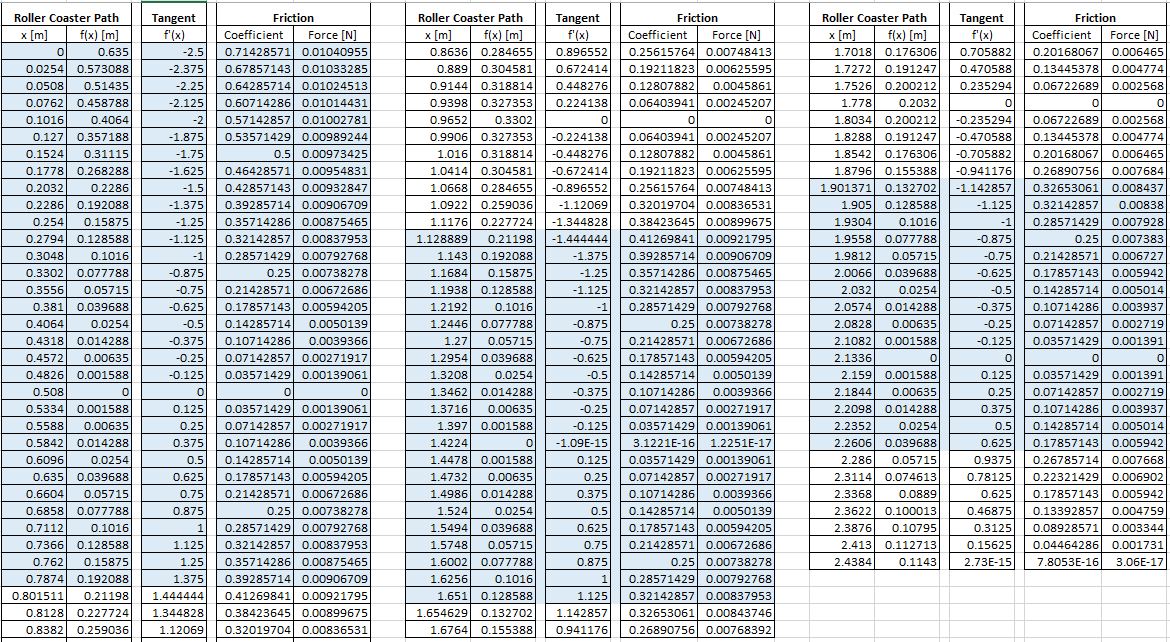
By definition, the friction force is proportional to the normal component of the body’s weight, and the constant of proportionality is the coefficient of friction. But for a curved roller coaster path, the normal component changes at every point on the path, the same as the slope of the tangent line (Figure 12).
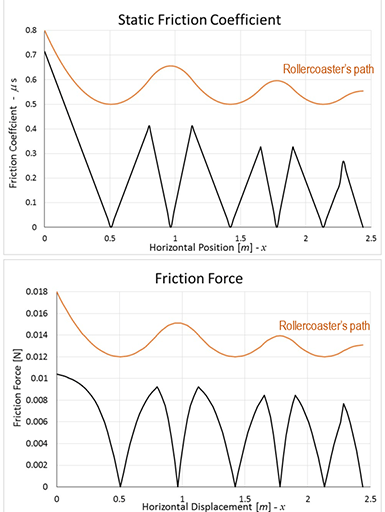
Notice also that the friction coefficient and the friction force are always considered positive because the friction force always opposes the body’s movement (Figure 12). In the work-energy equation obtained in the associated lesson, A Tale of Friction:
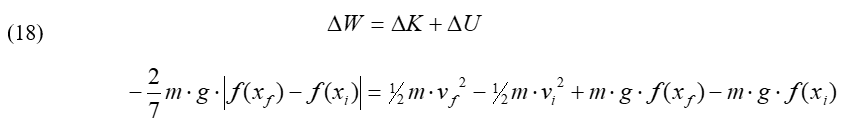
Before the Activity
- This activity and its associated lesson is suitable for the end of the first semester of the school year for high school AP Calculus courses, serving as a major grade for the last six-week period with the results presentation-report taken as the first-semester finals test.
- Before beginning this activity with students, practice every one of the steps described in the Background section, especially the calculations and graphs in the Rolling with Friction Calculations Example (an Excel® file). Notice that a Rolling with Friction Calculations No Calculus Example is also provided. Feel free to contact the author with any questions or suggestions.
- It is recommended that you create a working roller coaster model of your own to show to students.
- Arrange for an open work space where students have plenty of room to work.
- Make sure every team has access to a computer with Excel® and PowerPoint® (or similar/equivalent) software applications.
- Define which of the necessary construction materials you will provide and which you will ask students to provide.
- Teach the associated lesson, A Tale of Friction, making sure that students understand the equations they need to use to conduct this activity.
- Make copies of A Frictional Roller Coaster Pre-Quiz (one per student) and A Frictional Roller Coaster Project Rubric (one per team). Decide on a presentation-report deadline date and put that into the rubric before making copies of it.
- Before beginning the activity, administer the pre-quiz to students to provide practice and review in creating differentiable piecewise functions.
- Be ready with a computer, software and projector to show students the A Frictional Roller Coaster Presentation, a PowerPoint® file.
With the Students—Day 1: Activity Introduction (50 minutes)
- Present the Introduction/Motivation content to the class, using the accompanying slide presentation.
- Explain the overarching engineering design challenge and the specifics of what students need to do.
- Show students an example working roller coaster track prototype so they have some idea of what they might construct.
- Make it very clear that this is not another elementary-middle school roller coaster project like they may have done in the past or like the ones they saw in the linked videos. In this project, they cannot undo-redo the model to make it work. The entire path must be defined mathematically through a function, and their functionality supported with calculations before teams construct the roller coaster models.
- If some students ask if a ripple may be included in the roller coaster paths their teams design, answer as follows: A ripple requires more complex math expressions for the path (remind them that loops are not functions) and the computations involving velocity and friction require the incorporation of additional physics concepts like centripetal forces and accelerations. It is important to first understand perfectly well all the concepts and calculations in this project, before introducing loops into roller coaster paths. So we are not permitting loops in the designs for this project.
- Let students organize themselves in teams of three or four students each.
- Tell students what materials are provided and what materials they are to bring from home.
- Hand out the rubric.
With the Students—Day 2: Path Design (50 minutes)
- Ask students to define the initial heights and slopes of their coaster paths, and then use those numbers to find the equation of the first upward-opening parabola. They can also define the equations for parabolas 3 and 5, placing them at reasonable distances from parabola 1, depending on the planned model span (Figure 5).
- Then, using formula (1) and Excel®, direct the groups to each determine the maximum height the marble is able to reach after being dropped from the initial height. This height gives them what they need to define the height of the vertex of the second parabola (the first downward-opening parabola).
- Next, student find the equation of parabola 2, which is mid and tangent to parabolas 1 and 3.
With the Students—Day 3: Path Design (50 minutes)
- Students, again using equation (1), determine the maximum height the marble may reach when dropped from highest point and rolled through the parabolas 1-2-3 path.
- Have groups define the vertex height of parabola 4 (the second downward-opening parabola) and find the corresponding equation.
- Have teams determine the maximum height the marble may reach at the end of parabolas 1-2-3-4-5. Students may decide to either end the coaster’s path at that point or define a sixth parabola. Encourage them to include a sixth parabola. Instruct students to generate graphs for the designed path and for the expected velocities along the path (Figure 9).
- Note: Depending on students’ physics background and available time, ask them to generate graphs for the friction forces along the path.
With the Students—Days 4-6: Model Construction (50 minutes)
- Have students begin model construction using the final design dimensions they calculated during the previous work days.
- Use the pipe insulation material to build the physical models. This material is inexpensive and easy to work with. Remind students that the prototype model must match the design dimensions.
- To hold together and stabilize the physical model, have teams use cardboard sheets, masking tape, and vinyl L-bracket (corner bead) supports (see Figure 17).
- Permit teams to use different kinds of materials, but require students to first inform the teacher about any intended changes/additions.
- Suggest that students take photographs or videos of the various construction stages to include in their final presentations-reports (refer to the rubric).
- Require groups to test their models at least 10 times, recording the results. Direct the teams to draw conclusions about their designs and their physical models. Ask: Is the model behaving as expected? If not, why not and what conclusions can be made? What were the failures? What might explain the discrepancies/failures? How did you solve them?
- Model construction tips:
- Use a large cardboard (or plastic) sheet as the backing for each two-dimensional coaster path. If you only have smaller cardboard pieces, it works well to make a 3 x 4-ft backing by taping them together, edge-to-edge, rather than overlapping them. To aid in storage and transport, tape the sheets together such that they can be folded at the joints (see Figure 13).

- Split the pipe insulation in half lengthwise and use glue and tape to join together the split segments (see Figure 14) to make long coaster rails. Be careful to not let glue or tape get on the interior channel of the pipe insulation because that interferes with the rolling marble.

- To sketch the designed coaster path on the joined-together cardboard (or plastic) sheets requires some precise points. One easy and accurate way to draw the points is to use pegboard with a grid of one-inch-apart drilled holes (see Figure 15). Start by drawing a coordinate axis on the cardboard backing (15A). Then align two perpendicular lines of pegboard holes with the xy-axes drawn on the cardboard (15B, 15C). Use the pegboard holes to help graph points on the cardboard for the integer coordinates (or almost-integer coordinates; consider 14.05 or 14.1 to be “14”) of the designed coaster path (15D). Move along the horizontal axis of the pegboard to continue drawing points. Then sketch the coaster path by drawing lines to join the points.

- Cut the vinyl corner bead into one-inch pieces. These 90°-angle pieces (or any other system you devise) serve as L-brackets to support the pipe insulation channel—the coaster’s rail. Tape them at intervals along and parallel to the sketched path (Figure 16).

- Then use small pieces of rolled tape to adhere the pipe insulation channel onto the L-bracket supports made of corner bead pieces (Figure 17). Doing this completes the mathematically designed Russian Mountain roller coaster path prototype so it is ready for testing.

- To test the design functionality, use glass marbles as the roller coaster carts. It is important to use marbles with a diameter that is smaller than the pipe insulation’s inner diameter because all the calculations are based on using marbles that have only one point of contact with the coaster rail surface so the friction effect is as described in formula (1). A bigger marble will have many contact points and consequently more friction than what was considered in the calculations.
Day 7: Prepare and Present Project Report (50 minutes)
After school/on their own time, have each group create a slideshow or video to present to the rest of the class the different steps of its “professional engineering” work. Let students select and organize the information to include in the presentation-report, guided by the rubric. See the Assessment section for more information.
Vocabulary/Definitions
acceleration: The change in the velocity of an object. The average acceleration is defined as the change in velocity divided by time. The instantaneous acceleration is defined as the acceleration at any particular time period. In calculus, given the velocity of a body as a function of the time, the instantaneous acceleration is the derivative if the velocity with respect to the time.
continuous function: In a very basic approach, a function whose graph does not have any void and/or it is not broken, that is, can be drawn without lifting the pencil from the paper. More formally, a function is continuous at a point in its domain if a sufficiently small change in the input results in an arbitrarily small change in the output. In calculus, a function is continuous at a point x = c if and only if all the next three conditions are met: 1) the function is defined at x = c, 2) the limit of the function at x = c exists, and 3) the limit and the value of the function at x = c are equal.
derivative: The limit of the ratio of the change in a function to the corresponding change in its independent variable as the latter change approaches zero. Geometrically, this rate of change gives the slope of the tangent line at a point on the function’s graph. The graph of the function at that point must be continuous and smooth, that is, the function cannot have a peak at this point.
differentiable function : A function whose derivative exists at each point in its domain. Geometrically, the function whose graph is continuous and smooth such that a tangent line exists for every point on the graph.
energy conservation: A principle that states that in a system that does not undergo any force from outside the system, the amount of energy is constant, irrespective of its changes in form.
friction: The resistance to motion of one object moving relative to another. The surface resistance to relative motion, as of a body sliding or rolling. The force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other.
gravitational force: The force of attraction between masses; the attraction of the earth’s mass for bodies near its surface. The gravitational force between two bodies is proportional to the product of their masses and inversely proportional to the square of the distance between them.
inertial force: A force that resists a change in velocity of an object. It is equal to the applied force, but with opposite direction. Because of this force, every object in a state of uniform motion, or rest, tends to remain in that state unless an external force is applied to it.
kinetic energy: The energy possessed by an object due to its motion or movement. It is proportional to its mass and to the square of its velocity. The magnitude of this energy arises from the net work done on the object, to accelerate it from rest to its final velocity. Kinetic energy can be transformed again in work.
kinetic friction: A force that acts between moving surfaces. It is also known as sliding friction or moving friction, and it is the amount of retarding force between two objects that are moving relative to each other.
maximum of a function: The largest value of a function, either within a given range or on the entire domain. Formally, a function f (x) has a maximum at x = c, a < c < b, [a, b] a subinterval of the function’s domain, if f I > f (x), for a ≤ x ≤ b.
mechanical energy: The capacity of a physical system to change an object’s state of motion.
mechanical work: The amount of energy transferred by a force that moves an object. The work is calculated by multiplying the applied force by the amount of movement of the object.
minimum of a function: The smallest value of a function, either within a given range or on the entire domain. Formally, a function f (x) has a minimum at x = c, a < c < b, [a, b] a subinterval of the function’s domain, if f I< f (x), for a ≤ x ≤ b.
parabola: A conic section formed by the intersection of a vertical cone by a plane parallel to the cone’s side. A curve where any point is at an equal distance from a fixed point, the focus, and a fixed straight line, the directrix.
parabola vertex: The point where a parabola crosses its axis of symmetry. It is the maximum point when the parabola opens downwards, or the minimum point if the parabola opens upwards.
piecewise function: A function that is defined by multiple sub-functions, each sub-function applying to a certain interval of the main function’s domain. Also known as a hybrid function.
potential energy: The energy possessed by a body by virtue of its position relative to others. In a gravitational field, potential energy is the energy stored in an object as the result of its vertical position or height. The energy is stored as the result of the gravitational attraction of the earth for the object.
roller coaster: An amusement park ride that consists on an elevated railroad track designed with sharp curves and steep slopes on which people move in small, fast and open rolling cars.
Russian Mountains: The oldest roller coaster design and a predecessor to the modern day roller coaster. Descended from Russian winter sled rides on hills of ice, these early roller coasters were open wheeled carts or open train carts on tracks of elevated up-hills and down-hills supported by wooden or steel structures.
secant line: The straight line joining two points on a curve.
static friction: The friction that exists between a stationary object and the surface on which it rests—the force that keeps an object at rest and that must be overcome to start moving an object. Pushing horizontally with a small force, static friction establishes an equal and opposite force that keeps the object at rest.
system of equations: A set of equations working together at once. Systems of equations are called linear if all the equations in the system are linear (their graphs are all straight lines). Systems of equations are called non-linear if at least one of the equations in the system is not linear. Also called simultaneous equations.
tangent line: The straight line that touches a curve at a point without crossing over.
velocity: The time rate of change of position of a body in a specified direction. The average velocity is defined as the change in position divided by the time of travel. The instantaneous velocity is simply the average velocity at a specific instant in time. In calculus, given the position of a body as a function of the time, the instantaneous velocity is the derivative of the position with respect to the time
work-energy theorem: A principle that states that the work done by all forces acting on a particle equals the change in the particle’s kinetic energy.
Assessment
Pre-Activity Assessment
Pre-Quiz: Before beginning the activity, administer A Frictional Roller Coaster Pre-Quiz to students as practice in creating differentiable piecewise functions. Before moving on to conduct the activity, verify that every student is able to create a differentiable piecewise function joining two parabolas.
Activity Embedded Assessment
Checking In: During path design days, verify that students understand how to apply formula (1) to the path created with parabolas. Check their computations in their Excel® files.
Post-Activity Assessment
Professional Results Presentations: Along with their working roller coaster models, have teams prepare (after school and on their own) and present slide or video presentations to the class that summarize the process from design to calculations to prototype construction, including an overall analysis of the work done, problems encountered/resolved, and conclusions. This includes groups answering questions about why their models might not have performed exactly as expected; see the Investigating Questions section. Refer to the Project Rubric for expectations and grading suggestions.
Making Sense: Have students reflect about the science phenomena they explored and/or the science and engineering skills they used by completing the Making Sense Assessment.
Investigating Questions
During the final presentations, engage each team to reflect on why their models might not have performed exactly as expected. Many of these issues stem from the construction process and the difficulty in fabricating models that have the exact calculated dimensions (theory vs. reality). Suggested questions are provided below, along with example/possible student answers.
Q: What construction problems did you encounter?
A: It was difficult to evenly cut the pipe insulation in half lengthwise.
A: It was a challenge to place the half-pipe channel in the exact calculated positions. We had to estimate where to tape the vinyl holders/brackets and their inclinations so that the pipe insulation would pass through all the desired points with the required slope. A slightly misplaced holder affects the path’s shape.
A: It is difficult to place the pipe insulation channel with precision of less than one-quarter inch.
Q: What surprise, unanticipated (not considered) details did you encounter during construction?
A: A way to keep vertical and stable by itself the cardboard backing used to hold the coaster path.
A: The cardboard has a bit of curvature so the path is “not exactly” two dimensional.
A: If the pipe insulation was slightly twisted, it could cause a marble to fly away.
Q: Did your prototype model behave as expected?
A: In general, it behaved as expected—the marble passed all the hills—but its velocity at the end of the path was higher than the expected “almost zero” velocity.
Q: If not behaving as expected, why? What conclusions can be made?
A: The path hill heights were set lower than the maximum calculated heights, so the velocity of the marble along the path was always greater than the calculated velocity.
Q: What were some failures and their solutions?
A: The model failed if we were not careful with the way the marble was dropped at the beginning of the path. If not dropped smoothly, the marble may bounce past the first inches of the path, not attain the calculated velocity and not pass the first hill. So we needed to be careful to place and release the marble gently.
A: The model failed when we used a marble of diameter equal to the pipe insulation internal diameter. In this case, the friction on the marble is more because many points of contact exist, instead of just one, as estimated in the calculations, and then the marble stops sooner. So we made a point to always use marbles with diameters less than the pipe insulation internal diameter.
Troubleshooting Tips
You are welcome to contact the author, Miguel R. Ramirez, at mramirez2@galenaparkisd.com or 832-386-2922 to ask any questions related to this activity.
Activity Scaling
For lower grades, make simplifications in the path design process, but not in the physics or calculations to test the models. Instructor guidance for this approach:
- Have students with no calculus background draft by hand the roller coaster path, while keeping the same restrictions: no loops and a simple Russian Mountain path composed of parabola-like curves.
- For the calculations, use the Rolling with Friction Calculations No Calculus Example so that students do not have to perform the complex calculations by themselves. Graphs of the path, values, the rolling marble’s velocities along the path, and approximated friction values, are automatically displayed. Formula (1) is included in this worksheet to test design functionality.
- Have students draft their roller coaster paths by hand on graph paper and determine the x-y coordinates of points on the path (Figure 18A). Remind them that the drawings they make also serve as scaled blueprints of the models they will create, and suggest they use a 1-unit: 1-inch scale. Then direct them to enter these sketch coordinates into the no calculus spreadsheet in the x-y-columns in worksheet Path. Then, the designed path appears as a graph next to these columns (18B). The path is still a sequence of straight segments but it is softened in the graph.
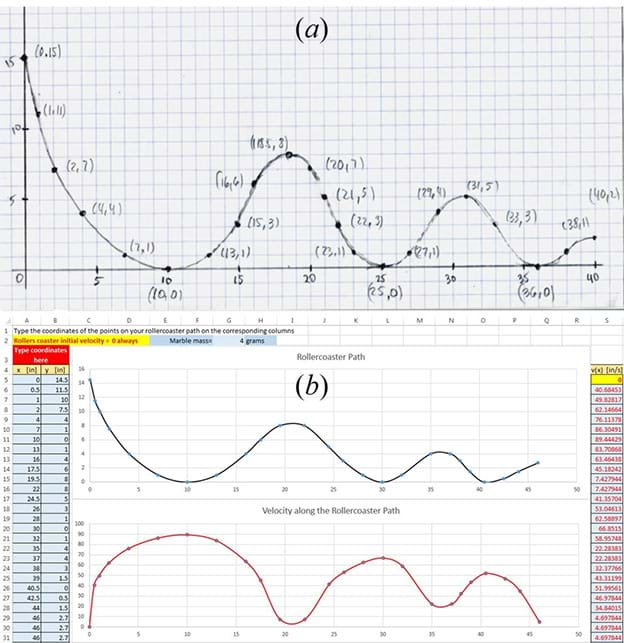
In addition, the velocities along the path are automatically calculated and displayed. The velocities are graphed below the path’s graph, and the values are displayed in a column to the right of the graphs (Figure 18B).
Changes made in the x-y column values are immediately displayed on the path’s graph, enabling students to see whether or not their changes produce an odd path. Expect students to use the process of set points > check > modify > visualize, until a functional path is obtained.
Any #NUM! error that shows up for an entry in the velocities column indicates a point corresponding to that entry where the body/marble stops rolling, indicating that the design requires modification for that portion.
The no-calculus spreadsheet also estimates the friction force along every segment of the path using a non-calculus alternative to formula (15):
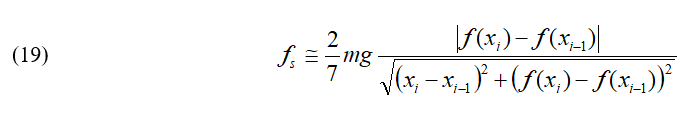
- Depending on your students’ math and physics background, decide how much of the associated lesson is convenient to teach. Even if the students are not ready for the entire lesson, you must present formula (1) to them because it is the main tool to check whether the designs work or not. To understand this formula and why the spreadsheet works, students must understand that:
- Friction is a non-conservative or dissipative force. It always opposes movement and its effect can be measured by evaluating the work it does. For a solid sphere rolling on an inclined straight surface, the work done by friction is proportional to the weight of the object and the surface steepness (19).
- When friction is present, the mechanical energy (ME) of a system: kinetic energy (K) + potential energy (U), is not constant. The work-energy theorem (18) states that the ME losses are equivalent to the work done by the friction force.
- The velocity of a solid sphere rolling on an inclined surface (1), can be determined using the work-energy theorem (18)
- A final recommendation: Use of the provided spreadsheet requires basic Excel® knowledge. The teacher must be familiar with this spreadsheet before the activity. The spreadsheet is designed to hold up to 40 points but can be modified as needed.
Additional Multimedia Support
Project support AP Calculus First Semester Project online tutorial for students at Sophia (by the author): https://www.sophia.org/playlists/ap-calculus-first-semester-project, on the following topics:
- Friction concepts and solutions for the problem of a body rolling on a surface with friction
- Rotational kinematics and dynamics
- Piecewise differentiable functions
Project support for Excel® and PowerPoint®:
Excel: Get Started with Formulas and Functions. Microsoft Office Support. https://support.office.com/en-us/article/Get-Started-with-Formulas-and-Functions-e0b10c56-700c-4961-a7b2-a0fc5866735e
Tips for Making Effective PowerPoint Presentations. May 28, 2009. National Conference of State Legislatures. http://www.ncsl.org/legislators-staff/legislative-staff/legislative-staff-coordinating-committee/tips-for-making-effective-powerpoint-presentations.aspx
Microsoft PowerPoint Tutorials. Electric Teacher. http://www.electricteacher.com/tutorial3.htm
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

Students explore the physics exploited by engineers in designing today's roller coasters, including potential and kinetic energy, friction and gravity. During the associated activity, students design, build and analyze model roller coasters they make using foam tubing and marbles (as the cars).
References
Alonso, Marcelo, & Edward, Finn. Fundamental University Physics, Volume 1 Mechanics. Addison-Wesley, 1966 (Spanish version: Fisica Volumen 1, Mecanica. Fondo Educativo Interamericano, 1976).
Briggs, William L., Cochran, Lyle, and Gillett, Bernard. Calculus AP Edition. Upper Saddle River, NJ: Pearson Education, 2014.
Brooks, Meade. Physics Concepts in Action | Physics Roller Coaster. 2014. Collin College, Frisco, TX. http://iws.collin.edu/mbrooks/student%20research/projects/Rollercoaster%20Simulation/index.html
Demana, Franklin, et al. Precalculus, Graphical, Numerical, Algebraic. Second Edition. Pearson, 2016.
Design a Roller Coaster (step by step applet). 2016. Amusement Park Physics: What are the forces behind the fun? Annenberg Foundation. https://www.learner.org/exhibits/parkphysics/coaster/
Giancoli, Douglas C. “Energy dissipation (friction) in a roller coaster.” Physics for Scientists and Engineers with Modern Physics. Google Book. Pp. 198. (R1) https://books.google.com/books?id=xz-UEdtRmzkC&pg=PA198&lpg=PA198&dq=energy+dissipation+in+a+roller+coaster&source=bl&ots=3N9n_vS6HA&sig=yKGlmZOWOrKKzfgw31vSMT_Bq6s&hl=en&sa=X&ved=0ahUKEwibroKfv7jSAhVETCYKHaalCl04KBDoAQgjMAI#v=onepage&q=energy%20dissipation%20in%20a%20roller%20coaster&f=false
Halliday, David, & Resnick, Robert. Physics, Parts 1 and 2 Combined. Second Edition. John Wiley & Sons, Inc., 1966 (Spanish version: Fisica, Edicion Combinada Partes I y II, CECSA, Tercera Edicion, 1976).
Harris, Benson. University Physics. Second Edition, John Wiley & Sons, Inc., 1995.
How Do Roller Coasters Work? Wonder of the Day #1239. Physical Science, Science, Wonderopolis.org. National Center for Families Learning. http://wonderopolis.org/wonder/how-do-roller-coasters-work
Larson, Ron, Edwards, Bruce, and Hostetler, Robert P. Calculus of a Single Variable. Eighth Edition. Boston, MA: Houghton-Mifflin, 2006.
Liddle, Scott. Physics of Roller Coasters (lesson). 2007. TeachEngineering Digital Library. https://www.teachengineering.org/lessons/view/duk_rollercoaster_music_less
Liddle, Scott: Building Roller Coasters (activity). 2007. TeachEngineering Digital Library. https://www.teachengineering.org/activities/view/duk_rollercoaster_music_act
Morrow, Mandy. The 10 Most Expensive Roller Coasters in the World. The Richest. June 11, 2014. http://www.therichest.com/luxury/most-expensive/the-10-most-expensive-roller-coasters-in-the-world/
Neumann, Erik. Roller Coaster (physics, equations, graphs; great interactive applet to make custom roller coasters). Last revised June 5, 2017. MyPhysicsLab.com. http://www.myphysicslab.com/roller/roller-single/roller-single-en.html
Pownal, Malcom. Functions and Graphs, Calculus Preparatory Mathematics, Prentice-Hall, 1983.
Roller Coaster Physics. Real-World Physics Problems.com. http://www.real-world-physics-problems.com/roller-coaster-physics.html
Sastamoinen, Shawna. Roller Coaster Physics: The Science Behind the Thrills. 2002. Physics 211X, University of Alaska Fairbanks. http://ffden-2.phys.uaf.edu/211_fall2002.web.dir/shawna_sastamoinen/Roller_Coasters.htm
Young, Hugh D., & Freedman, Roger. University Physics with Modern Physics.14th Edition, Pearson, 2016.
Copyright
© 2017 by Regents of the University of Colorado; original © 2017 Miguel R. RamirezContributors
Miguel R. Ramirez, Galena Park High SchoolSupporting Program
Miguel R. Ramirez, high school math teacher, Texas, USAAcknowledgements
The author expresses his thanks to Tony Gardea, Galena Park High School Principal; Seretha Augustine, Galena Park High School Associate Principal for Curriculum; and Gerard Kwaitkowski, Galena Park High School Math Specialist.
Last modified: February 11, 2022







User Comments & Tips