Quick Look
Grade Level: 7 (6-8)
Time Required: 45 minutes
Lesson Dependency: None
Subject Areas: Physical Science
Summary
Students are introduced to the five fundamental loads: compression, tension, shear, bending and torsion. They learn about the different kinds of stress each force exerts on objects.
Engineering Connection
Engineers take into consideration the impact of many types of forces when designing structures. Factors that influence the design decisions include: anticipated use of the structure, expected weather exposure, and the type of soil it will be built upon. Engineers choose the best materials and design approaches for buildings and machines by calculating how much, and what kind of stresses each material is able to withstand without failure.
Learning Objectives
After this lesson, students should be able to:
- Identify the five fundamental loads: compression, tension, shear, bending and torsion.
- Explain the concept of a moment and how to calculate one.
- Explain how moments create bending and torsion loads on structures
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.
(Grade
6)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Improve essential skills necessary to successfully design.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Massachusetts - Science
-
Describe different ways in which a problem can be represented, e.g., sketches, diagrams, graphic organizers, and lists.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
-
Identify relevant design features (e.g., size, shape, weight) for building a prototype of a solution to a given problem.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
-
Explain how the forces of tension, compression, torsion, bending, and shear affect the performance of bridges.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Identify and explain the steps of the engineering design process, i.e., identify the need or problem, research the problem, develop possible solutions, select the best possible solution(s), construct a prototype, test and evaluate, communicate the solution(s), and redesign.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Describe and explain the purpose of a given prototype.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Identify appropriate materials, tools, and machines needed to construct a prototype of a given engineering design.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
Introduction/Motivation
Have you ever wondered why skyscrapers don't fall over? Why bridges don't sink into the rivers they span, or why bicycles are different sizes and shapes? Why are some buildings made of wood and others are made of steel and glass? That's easy! Because they are made that way right?
Well, how do the people who design things know which material is best to use, how tall a building can be, or even where the best place is to put a bridge? Engineers design structures, such as buildings, dams, airplanes, automobiles, tunnels, chairs, bicycle frames and even toys to hold weight and withstand forces that are placed on them that could tear them apart. So what is a force?
We all know from experience that a force is the amount of pushing or pulling required to move an object. Engineers determine the loads or external forces that act upon a structure. When external forces are applied to a structure, internal stresses (internal forces) develop resistance to the outside forces. The opposition of external and internal forces is what holds the structure together. Once engineers know the loads acting on a structure, they calculate the resulting internal stresses, and design each piece of the structure so it is strong enough to carry the loads without breaking. Students can act as engineers by illustrating tension, compression and torsion in the Forces in Structures: Glue Sticks Bend & Twist activity.
Lesson Background and Concepts for Teachers
The five types of loads that can act on a structure are tension, compression, shear, bending and torsion.
- Tension: Two pulling (opposing) forces that stretch an object trying to pull it apart (for example, pulling on a rope, a car towing another car with a chain – the rope and the chain are in tension or are "being subjected to a tensile load").

Figure 1. Tension.
- Compression: Two pushing (opposing) forces that squeeze an object trying to compress it (for example, standing on a soda can, squeezing a piece of wood in a vise – both the can and the wood are in compression or are "being subjected to a compressive load").

Figure 2. Compression.
- Shear: Two pushing or pulling adjacent forces, acting close together but not directly opposing each other. A shearing load cuts or rips an object by sliding its molecules apart sideways (for example, pruning shears cutting through a branch, paper-cutter cutting paper - the branch and paper are "subjected to a shear loading").

Figure 3. Shear.
Another example: Pulling on two pieces of wood that have been glued together; the glue joint is "being subjected to a shear loading." 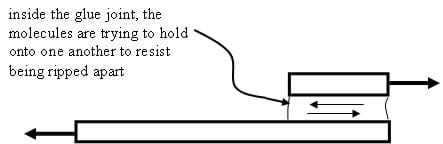
A Moment of a Force
Understanding a moment of a force is key to understanding the last two types of loads. A moment is a "turning force" caused by a force acting on an object at some distance from a fixed point. Consider the diving board sketch in Figure 5. The heavier the person (force), and the farther they walk out on the board (distance), the greater the "turning force," which acts on the concrete foundation (fixed point).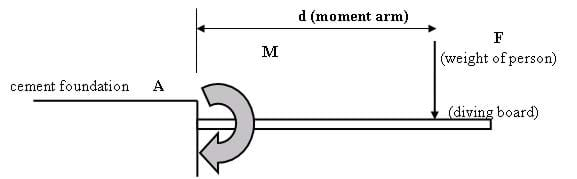
The force (F) produces a moment or "turning force" (M) that tries to rotate the diving board around a fixed point (A). In this case, the moment bends the diving board.
The stronger the force, and the greater the distance at which it acts, the larger the moment or "turning force" it will produce.
A moment or "turning force" (M) is calculated by multiplying a force (F) by its moment arm (d). The moment arm is the distance at which the force is applied, taken from the fixed point: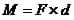
(As long as the force acting on the object is perpendicular to the object.)
If a force measured in Newtons is multiplied by a distance in meters, then the units for the moment are N-m (read "Newton-meters"). If the force is measured in pounds and multiply by a distance in inches, then the units are be lb-in (read "pound-inches"). Units for moments can be any force unit multiplied by any distance unit.
- Bending: When a moment or "turning force" is applied to a structural member that is fixed on both ends, such as a pole beam, making it deflect or bend. A moment that causes bending is called a bending moment. Bending produces tension and compression inside a beam or a pole, causing it to "smile." The molecules on the top of the smile get squeezed together, while the molecules on the bottom of the smile get stretched out. A beam or pole in bending will fail in tension (break on the side that is being pulled apart) (for example, a shelf in a bookcase, and the earlier diving board scenario).
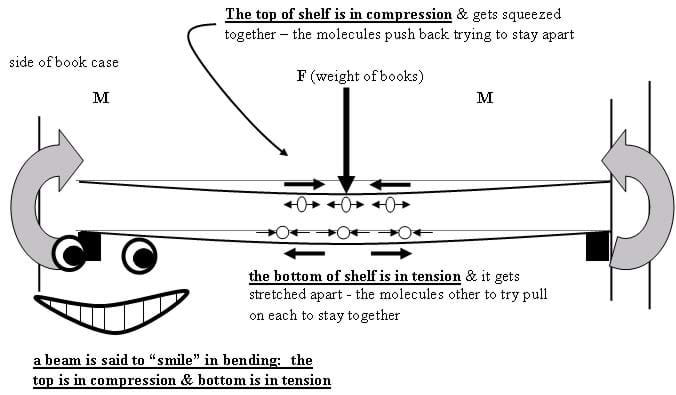
Figure 7. A bookcase example of bending.
- Torsion (Twisting): Created when a moment or "turning force" is applied to a structural member (or piece of material) making it deflect at an angle (twist). A moment that causes twisting is called a twisting or torsional moment. Torsion produces shear stresses inside the material. A beam in torsion will fail in shear; the twisting action causes the molecules to be slid apart sideways (for example, a pole with a sign hanging off one side).
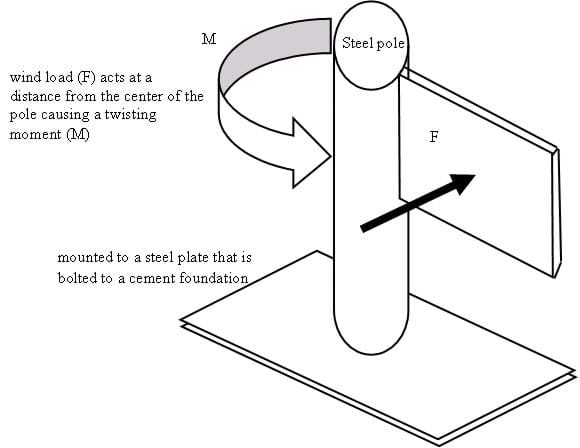
Figure 8. Torsion.
Associated Activities
- Forces in Structures: Glue Sticks Bend & Twist - Students use glue sticks to demonstrate tension, compression and torsion.
Assessment
Questions: Evaluate students' understanding of the material, individually or as a group, using the Investigating Questions provided in the associated activity.
Problem 1: Calculate the moment resulting when a person weighing 150 lbf stands at the end of a 120 in. diving board (use the moment equation: M = F x d) (Answer: 18,000 lbf-in.)
Problem 2: If 1 N = 0.2248 lbf and 1m = 3.28 ft, convert the units in the previous problem to obtain a solution in Nm (Answer: 18,000 lbf-in. x 1 N / 0.2248 lbf x 1 ft / 12 in. x 1 m / 3.28 ft = . 203 Nm)
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn about torsion as a force acting upon structures and have the opportunity to design something to withstand this force.

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...

To introduce the two types of stress that materials undergo — compression and tension — students examine compressive and tensile forces and learn about bridges and skyscrapers. They construct their own building structure using marshmallows and spaghetti to see which structure can hold the most weigh...
Other Related Information
Browse the NGSS Engineering-aligned Physics Curriculum hub for additional Physics and Physical Science curriculum featuring Engineering.
Copyright
© 2013 by Regents of the University of Colorado; original © 2005 Worcester Polytechnic InstituteContributors
Douglas Prime, Tufts University, Center for Engineering Educational OutreachSupporting Program
K-12 Outreach Office, Worcester Polytechnic InstituteLast modified: October 30, 2023





User Comments & Tips