Quick Look
Grade Level: 5 (4-6)
Time Required: 45 minutes
Expendable Cost/Group: US $5.00 This activity uses some non-expendable (reusable) items, such as LEGO MINDSTORMS robots and software; see the Materials List for details.
Group Size: 4
Activity Dependency: None
Subject Areas: Measurement, Physics, Science and Technology
NGSS Performance Expectations:

| 3-5-ETS1-2 |

Summary
Students work as engineers and learn to conduct controlled experiments by changing one experimental variable at a time to study its effect on the experiment outcome. Specifically, they conduct experiments to determine the angular velocity for a gear train with varying gear ratios and lengths. Student groups assemble LEGO® MINDSTORMS® EV3 robots with variously sized gears in a gear train and then design programs using the EV3 software to cause the motor to rotate all the gears in the gear train. They use the LEGO data logging program and color sensors to set up experiments. They run the program with the motor and the color sensor at the same time and analyze the resulting plot in order to determine the angular velocity using the provided physics-based equations. Finally, students manipulate the gear train with different gears and different lengths in order to analyze all these factors and figure out which manipulation has a higher angular velocity. They use the equations for circumference of a circle and angular velocity; and convert units between radians and degrees.Engineering Connection
The concept of angular velocity is used in engineering applications every day, from car wheels to orbiting spacecraft. The magnitude of angular velocity is the angular speed of an object as it rotates about a specified axis, measured in radians per second. An understanding the angular velocity of objects can be used to determine how fast something rotates and to derive the angular acceleration, which can be used to determine the torque exerted on a body. One way of changing the angular velocity and the torque is by the use of gears. Mechanical engineers utilize gears in drive trains for a variety of applications ranging from bicycles to automobiles. Gears are used to transmit power, change the direction of power and alter the angular velocity and torque being applied to the output of a system. The angular velocity or torque can be modified by changing the gear ratio.
In this activity, students learn to design a setup for engineering experimentation. Specifically, they design their own robots, write their own robot programs and determine angular velocities. As they play with changing the robot design, they figure out what design features help increase angular velocity; they optimize angular velocity by changing gears and number of gears, and use the provided equations.
Learning Objectives
After this activity, students should be able to:
- Design a LEGO MINDSTORMS EV3 robot with a gear train.
- Program a LEGO robot using the EV3 software.
- Design a gear train with two different types of gears with a specified number of gears.
- Calculate the angular velocity of rotating gears using a color sensor to detect wheel rotation.
- Change one variable at a time and examine its effect on angular velocity.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
3-5-ETS1-2. Generate and compare multiple possible solutions to a problem based on how well each is likely to meet the criteria and constraints of the problem. (Grades 3 - 5) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Generate and compare multiple solutions to a problem based on how well they meet the criteria and constraints of the design problem. Alignment agreement: | Research on a problem should be carried out before beginning to design a solution. Testing a solution involves investigating how well it performs under a range of likely conditions. Alignment agreement: At whatever stage, communicating with peers about proposed solutions is an important part of the design process, and shared ideas can lead to improved designs.Alignment agreement: | Engineers improve existing technologies or develop new ones to increase their benefits, to decrease known risks, and to meet societal demands. Alignment agreement: |
Common Core State Standards - Math
-
Geometric measurement: understand concepts of angle and measure angles.
(Grade
4)
More Details
Do you agree with this alignment?
-
Use parentheses, brackets, or braces in numerical expressions, and evaluate expressions with these symbols.
(Grade
5)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Evaluate designs based on criteria, constraints, and standards.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
in a group setting, test their solution against design specifications, present and evaluate results, describe how the solution might have been modified for different or better results, and discuss tradeoffs that might have to be made.
(Grades
5 -
8)
More Details
Do you agree with this alignment?
-
extend mathematical notation and symbolism to include variables and algebraic expressions in order to describe and compare quantities and express mathematical relationships.
(Grades
5 -
8)
More Details
Do you agree with this alignment?
-
interpret the organized data to answer the research question or hypothesis and to gain insight into the problem.
(Grades
5 -
8)
More Details
Do you agree with this alignment?
New York - Science
-
Generate and compare multiple possible solutions to a problem based on how well each is likely to meet the criteria and constraints of the problem.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3
- LEGO MINDSTORMS Education EV3 Software 1.2.1, free online, you have to register a LEGO account first; at https://www.lego.com/en-us/mindstorms/downloads/download-software
- computer loaded with EV3 1.2.1 software
- LEGO MINDSTORMS EV3 color sensor, included in the core set listed above
- 2 LEGO MINDSTORMS EV3 intelligent bricks; one is included in the core set listed above; additional bricks are available at https://shop.lego.com/en-US/EV3-Intelligent-Brick-45500
- calculator
- ruler
- electrical tape, such as white or orange, not black; two pieces, each about 3 inches long.
- Angular Velocity Worksheet, one per student
- (optional) Example Experimental Setup Visual Aid (same image as Figure 1), suitable for an overhead projector transparency
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:
- LEGO MINDSTORMS NXT robot, such as the NXT Base Set
- computer loaded with NXT 2.1 software
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_angular_activity1] to print or download.Pre-Req Knowledge
Students should be comfortable working with multiplication and division, and have an understanding of the basic concept of a function.
Students and teachers should have previous basic experience programming LEGO robots, for example, as learned in the What Is a Computer Program? unit.
Introduction/Motivation
How many of you love to watch cars moving fast? Can you think of some times—maybe in real life, in a movie, on TV or on the Internet—that you have seen cars traveling really fast? (Call on a few students to share their experiences.) The term "speed" is often used to describe how fast objects move. In today's activity, we will try to determine how fast a set of gears turn on a gear train. Gears are important for the movement of vehicles. For example, engineers design gear trains for automobiles so they can travel at different speeds. This is what you will be doing in this activity, the same research and optimization work as engineers!
To determine how fast the gears turn, we will use a color sensor along with the LEGO EV3 software and data logging program. Then, we will adjust the types of gears and the length of the gear train and determine the angular velocity for each of the different types of gear trains. Then you will determine the optimal gear train, based on the fastest angular velocity achieved.
Who knows what I mean by "optimal"? (Listen to student explanations; correct and amend as necessary. Give some examples.) By optimal, we mean what is best suited for the situation.
In the process of this experiment, you will learn about all the math and science that is necessary to understand the angular velocity of gear trains. You'll get to make your own robotic creations and your own programs to cause robot gear trains to spin fast. By changing one variable at a time, you will determine which variable makes the gear train have the highest angular velocity. In doing so, you will also learn the importance of each variable to the experiment outcome.
Procedure
Physics-Based Equations Background
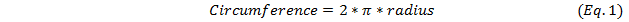
Circumference is the distance along the outside of a circle, otherwise known as the perimeter of a circle. It has a unit of length. The value for the radius is the distance from the center of the circle to the perimeter.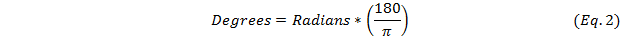
Degrees is the measure of the planar angle along a circle, thus a full circular rotation has a radian rotation of 2π, which is 360°.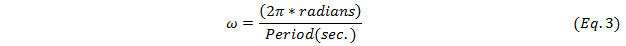
where ω is the angular velocity in degrees per second, and the period is the amount of time it takes the wheel to complete one rotation. The period can be determined using the EV3 data logging program. The steps to get the data logging to work are listed below (and provided in the Procedure > With the Students section). One period of rotation can be taken as the time between peaks on the resulting EV3 graph, as seen in Figure 2. The EV3 data logging steps:
- Under the "File" tab, press the "switch to EV3 Datalogging" button.
- In the "Start a new experiment" section, name your experiment, then press the go button.
- When asked to configure your experiment/data logging, set the duration for any appropriate time (start off with 15 seconds). Since the wheel could be moving fast, set the sampling rate to 25 samples per second, which is the maximum sampling rate.
- On the right side, select the port to which the color sensor is plugged into.
- Press OK; now you should be at the graph screen.
- Once you are ready to start recording data (wheels are spinning), press the "Download and Run" button, which looks like a standard "play" button.
Before the Activity
- Gather materials and make copies of the Angular Velocity Worksheet, one per student.
- (optional) If desired, project on the wall the Example Experimental Setup Visual Aid; the same image is also provided on the worksheet and as Figure 1.
- It is helpful to make your own experimental setup example and practice EV3 data logging in advance, so you are ready to help students troubleshoot their experiments. Note that one EV3 brick controls the data logging, while the other brick drives the gear train. Refer to a good example of data logging at https://ev3lessons.com/en/ProgrammingLessons/advanced/DataLoggingTemp.pdf and https://ev3lessons.com/en/ProgrammingLessons/advanced/DataLoggingTurns.pdf.
- Be ready to show students a three-minute online video; see the link in the Additional Multimedia Support section. It is helpful for teachers to watch this video in advance.
With the Students
- Present the Introduction/Motivation section content to the class.
- Introduce to students the concept of data logging. Data logging is using a computer to collect and record data over an extended period of time through the use of a sensor. This way, a person does not have to sit for hours on end collecting and recording data, since the computer can do it. As an example, you may have heard of the "black boxes" in all commercial aircraft; they are one example of a data logger. These flight data recorders collect and record all aircraft performance data that is sent and transmitted throughout the plane during flights. At a more basic level, the program in this activity accomplishes the same task; the EV3 brick takes data from the color sensors and stores the values as time progresses.
- Continue with an open class discussion to have students think of some other types of data loggers and their applications. (Examples: Many trains, ships and cars have data recorders, just like airplanes. Some cars, including race cars, have devices that collect data right before and after a crash, and keep track of other performance data for purposes of engine monitoring and service diagnostics. Those hoses laid on roadways to count the traffic of cars and bicycles at a specific location. The continuous 24/7 monitoring of earthquake tremors by seismographs. Pacemakers that continuously monitor electrical activity of the heart so that doctors can look back at their behavior over time. Trucks with acceleration sensors to monitor fragile and valuable goods during transport, measuring the shocks and vibrations experienced. Measuring the g-forces acting on people when riding rollercoasters [to design them so they are thrilling yet not harmful]. All sorts of other situations in which we want to automatically collect data from sensors over time, such as ongoing measuring and recording of temperatures, vibrations, humidity, light intensity, sequence of input/output events, GPS locations, factory emissions, patient monitoring, environmental conditions, avalanche monitoring, wind generator monitoring, crash testing.)
- As a class, review the LEGO MINDSTORMS EV3 data logging program and show students how the color sensor works in the program. Show students a EV3 data logging YouTube video at https://www.youtube.com/watch?v=wP58lVrDA6I. With students, go through the step-by-step process to begin recording and logging data:
- Under the "File" tab, press the "switch to EV3 Datalogging" button.
- In the "Start a new experiment" section, name your experiment, then press the go button.
- When asked to configure your experiment/data logging, set the duration for any appropriate time (start off with 15 seconds). Since the wheel could be moving fast, set the sampling rate to 25 samples per second, which is the maximum sampling rate.
- On the right side, select the port to which the color sensor is plugged into.
- Press OK; now you should be at the graph screen.
- Once you are ready to start recording data (wheels are spinning), press the "Download and Run" button, which looks like a standard "play" button.
- Teach students about circumference, units for circumference, velocity, and angular velocity. Review with them the physics-based equations, which are provided as Equations 1, 2 and 3 in the Procedure > Background section.
- Divide the class into groups of four or five students each and provide each team with the activity materials and space to work. In each team, assign each group member a task, so at least two are working on the program and two on the gear train setup. Hand out the worksheets.
- On the worksheet, review the vocabulary words and definitions, as needed.
- Direct students to write their own experimental hypotheses on their worksheets. Ask students: What do you think will happen to the angular velocity if you change the gear length and gear ratio in the gear train? Which gear sets do you expect to have the highest and lowest angular velocity?

Figure 1. An example robot design with color sensor and gear train for the purpose of determining angular velocity of gears. (Only one color sensor is necessary for this activity.) - Make sure students know that the LEGO color sensor takes in ambient light and is able to distinguish between dark and light colors. It can simply measure the intensity of the different lights and can be programmed to react to a particular intensity. For this experiment, we want the color sensor to detect how many times a strip of tape on the wheel (see the red tape in Figure 1) comes into the sensor's view. Then, the data logging software shows those instances on a time plot as spikes in the detected light intensity (see Figure 2).
- Have groups proceed to design their own LEGO MINDSTORMS EV3 gear trains and data logging devices to use for calculating angular velocity, using Figure 1 as an example (the same photograph is provided on page 1 of the worksheet). One EV3 brick controls the data logging, while the other brick drives the gear train. Indicate that the entire setup should look similar or be able to function like the example experimental setup in Figure 1: a servo motor drives one of the axles, a little stand holds the color sensor, and a structure supports a gear train of various gears and axles, which they will alter throughout the experimental testing. Creating the experimental setup serves as a key part of the activity, since independent problem solving is an important skill for engineers to master. (Note: Only one color sensor is necessary for this activity.)
- Have students work with the EV3 color sensor in the data logging program so they become familiar with the program and sensor (see step 4 if students get stuck). Direct groups to put together the entire experimental setup by:
- Attaching the color sensor to the brick and positioning them as shown in Figure 1.
- Connecting their gear trains to a LEGO servo motor with a taped wheel at the end, as shown in Figure 1. One or two wheels may be used. The tape on the wheel provides the contrast in color necessary to produce the peaks and valleys graphed from the color sensor data.
- Have students document on their worksheets (under the Procedure section) brief but accurate explanations, with sketches if they like, of the experimental setup they built and the steps they followed to construct the data logging device.

Set up the LEGO data logging program in conjunction with the color sensor to create the gear experimental setup. - Once groups have created their setups, show students examples of the various gears that are provided in the LEGO core set and have them make observations. Ask the students: How many teeth do the big, medium and small gears have? Have students measure the radii of the different gears. (Note: Measure the diameter from the outermost part of the gear teeth.)
- Then direct groups to start by creating gear trains with two gears of the same size.
- Next, have groups use the LEGO software to create EV3-G programs to drive the motor and collect data, referring to the YouTube EV3 data logging video (https://www.youtube.com/watch?v=Y8rt8ItuD3c) as needed. The programs should drive the servo motor for a certain amount of time at a certain power level with the drive motor connected to the gear train axles to spin the gears and the wheel (such as shown on Figure 1).
- Measure the period for each type of gear train using the data logging program, via the analysis tool in the top toolbar. One period of rotation is the time between peaks on the graph. (Note: The spacing between peaks indicates the relative angular velocity of the rotating wheel with smaller spacing indicating faster speeds and wider spacing indicating slower speeds.) Figure 2 shows an example of the resulting time plot expected, as well the length of one period.
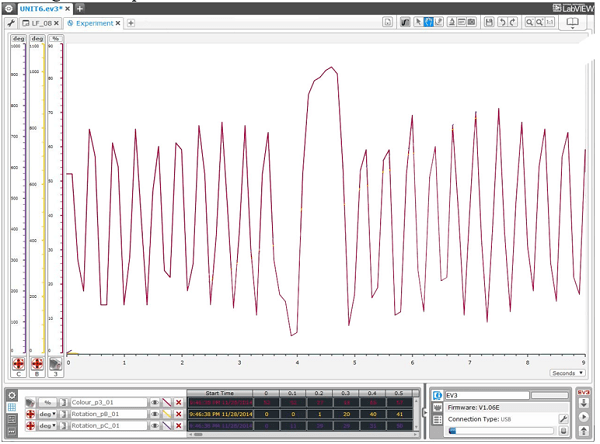
Figure 2. An example data logging experimental result in graphical form. The spikes on this time plot represent the sensor's detection of light intensity (the wheel strip spinning by), in other words, a counting of the LEGO wheel revolutions. One period of rotation is the time between peaks on the graph. The spacing between peaks indicates the relative angular velocity of the rotating wheel with smaller spacing indicating faster speeds and wider spacing indicating slower speeds. - As students collect data, have them fill out the worksheet. For example, when they measure the radius of a gear, have them calculate and record the circumference for that specific gear. Once data is collected from the data logger, have students fill out the corresponding section of the worksheet and then determine the angular velocities. The equations for circumference and angular velocity are provided on the worksheet, as well as the conversion equation for degrees/radians.
- Then, still using only two gears, have students experiment with a variety of different gear sizes (a big and a small) to explore a range of gear ratios. Let students tap their creative problem solving skills to get the gears to mesh correctly.
- Once students have mastered various combinations of two gears, direct them to begin adding more gears to the gear train. Have students test all the combinations provided on the second data table on the worksheet, all consisting of gear trains with four gears.
- Have students complete their worksheets, documenting their results and conclusions.
- Conclude by leading a class discussion, so students can share and discuss what they learned from the experiment. Review their results, observations, questions and conclusions. What setup was the fastest, which was the slowest? What happened when you added a bunch of gears? Which was optimal? Ask the Investigating Questions.
Vocabulary/Definitions
angular velocity: The rate of angular motion; the rate of change of angular displacement over time.
circumference: 1) The outer boundary (perimeter) of a circle. 2) The length of this line.
data logging: Using a computer to collect and record data over an extended period of time through the use of a sensor.
degree: The unit of measure for a given angle.
diameter: The length of a line segment passing through the center of a circle and intersecting both sides of the circle.
gear: A rotating disk or wheel with cut teeth. An assembly or arrangement of such parts into a group of parts or mechanism that performs one function in a machine.
gear ratio: The ratio of the angular velocity of the input gear to the output gear. This ratio can also be defined using the radii or the number of teeth of the gears.
gear train: A set of gears that is able to transfer rotational motion.
linear velocity : The distance traveled per unit time.
optimal: Best suited for the situation. The best choice, arrangement, result or decision obtainable that meets specific requirements.
perimeter: 1) The border or outer boundary of a two-dimensional figure. 2) The length of this line.
period: The length of time to complete one cycle.
radian: The unit of measure for a central angle between two radii of a circle. 1 radian = ~57.296 degrees. The measure of a circle is 2π radians = 360°.
radius: 1) A straight line segment from the center of a circle to its perimeter. 2) The length of this line. Plural is radii.
Assessment
Pre-Activity Assessment
Guessing Game: Before starting the experiment ask students to predict which set of gears in the two-gear train system will have the highest angular velocity.
Activity Embedded Assessment
Design a Robot: After students have made two-gear system gear trains, ask individual teams to show you how their gear trains work, including explaining what the gears do. (Answer: Expect students to touch on the main purposes of a gear train, which are to 1] transmit power and 2] change the angular velocity and torque being supplied to the wheels.)
Worksheet: Throughout the experiment, have students use the Angular Velocity Experiment Worksheet to write their hypotheses, document their procedures, record their data, calculate angular momentum, and answer questions about their results and conclusions. Review their completed worksheets to gauge their depth of comprehension. Example answers and teacher guidance are provided on the Angular Velocity Experiment Worksheet Answer Key.
Post-Activity Assessment
Tuning the Equation: After student groups have experimented by changing the gears in their gear trains and the lengths of the gear trains, ask them: What gear train is optimal for a high angular velocity? (Answer: A gear train with the highest ratio of the number of input teeth to output teeth has the largest gear ratio and is optimal for the highest angular velocity.)
Concluding Discussion: Lead a class discussion so students can share their results, observations, questions and conclusions. Ask the Investigating Questions. Use this opportunity to gauge student comprehension.
Investigating Questions
- Which gear train had the highest angular velocity for the two-gear system? Why? What is the gear ratio? (Answer: The gears with the largest input-to-output ratio have the highest angular velocity. For example, if the gear that is attached to the motor has 24 teeth and the gear attached to the wheels has 8 teeth, the gear train multiples the speed of the motor by a factor of 3.)
- What happened to the angular velocity when the length of the gear train was increased? (Answer: The system slows down due to friction, even if the gear ratios are the same. The additional gears and spinning axles creates more friction in the system.)
- For a four-gear train, what gear ratios are best to use in order to obtain a system with a high angular velocity? (Answer: The same principles apply as from the first question. Though, since this is a gear train with additional gears, it is a chance for students to get creative because they can multiply the gear ratios by making the output of the first set of gears the input to the next set of gears.)
Safety Issues
- Poking fingers into the gears when the EV3 programs are running could hurt.
Troubleshooting Tips
Make sure that the periods are accurately determined in the data logging program.
Activity Scaling
- For upper grades, require students to calculate the linear velocity of the wheel's outer surface. (velocity of a point on the circumference of the wheel) for various gear configurations. Use the following equation: linear velocity (cm/sec) = angular velocity (radians/sec) * radius (cm).
Additional Multimedia Support
Show students the YouTube video, Simple EV3 Data Logging, at https://www.youtube.com/watch?v=Y8rt8ItuD3.
See a list of data logger applications at http://en.wikipedia.org/wiki/Data_logger.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to gear transmissions and gear ratios using LEGO® MINDSTORMS® EV3 robots, gears and software. They learn how to build the transmission part of a vehicle by designing gear trains with different gear ratios. Once students learn the principles behind gear ratios, they are put to...

Students are introduced to an important engineering element—the gear. Different types of gears are used in many engineering devices, including wind-up toys, bicycles, cars and non-digital clocks. Students learn about various types of gears and how they work in machines.

Students analyze the relationship between wheel radius, linear velocity and angular velocity by using LEGO® MINDSTORMS® EV3 robots. Given various robots with different wheel sizes and fixed motor speeds, they predict which has the fastest linear velocity.
References
Hewitt, Paul G. Conceptual Physics. Upper Saddle River, NJ: Prentice Hall, 2002.
Zitzewitz, Paul W. Physics Principles and Problems. OH: McGraw-Hill, 2002.
Copyright
© 2014 by Regents of the University of Colorado; original © 2010 Polytechnic Institute of New York UniversityContributors
Jennifer S. Haghpanah, Leonarda Huertas, Jasmin Mejias, Mihai Pruna, James CoxSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: October 16, 2020





User Comments & Tips