Quick Look
Grade Level: 11 (9-12)
Time Required: 1 hours 30 minutes
(can be split into two 45-minute sessions)
Expendable Cost/Group: US $0.00 This activity also uses non-expendable (reusable) computers with JAVA and editing software, and Bluetooth devices, although the latter is not required; see the Materials List for details.
Group Size: 3
Activity Dependency: None
Subject Areas: Computer Science, Data Analysis and Probability
NGSS Performance Expectations:

| HS-ETS1-4 |

Summary
Students simulate disease transmission by collecting data based on their proximity to other students. One option for measuring proximity is by having Bluetooth devices "discover" each other. After data is collected, students apply graph theory to analyze it, and summarize their data and findings in lab report format. Students learn real-world engineering applications of graph theory and see how numerous instances of real-world relationships can be more thoroughly understood by applying graph theory. Also, by applying graph theory the students are able to come up with possible solutions to limit the spread of disease. The activity is intended to be part of a computer science curriculum and knowledge of the Java programming language is required. To complete the activity, a computer with Java installed and appropriate editing software is needed.Engineering Connection
Graph theory is the study of graphs in computer science and mathematics. A graph is a mathematical structure used to model relationships between the objects in a set of objects. In this context, graphs have vertices or "nodes" and a group of edges, which connect pairs of vertices. In computer science, software engineers use graphs to represent communication networks, data organization, computational devices and the flow of computation. One example of graph theory used by computer and software engineers is cell phone networks. Your phone is a node along with repeater towers and base stations. When you make a call, you connect with other nodes and those connections become edges in the graph. Another example is social networks that software engineers exploit on sites like Facebook to market products. By using graph theory, software engineers use the connections (edges) to your friends to find people who might also want to buy products of interest to you.
Learning Objectives
After this activity, students should be able to:
- Use graph theory to complete depth first search (DFS) and breadth first search (BFS).
- Analyze of the spread of disease using Graph theory concepts.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-4. Use a computer simulation to model the impact of proposed solutions to a complex real-world problem with numerous criteria and constraints on interactions within and between systems relevant to the problem. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Use mathematical models and/or computer simulations to predict the effects of a design solution on systems and/or the interactions between systems. Alignment agreement: | Both physical models and computers can be used in various ways to aid in the engineering design process. Computers are useful for a variety of purposes, such as running simulations to test different ways of solving a problem or to see which one is most efficient or economical; and in making a persuasive presentation to a client about how a given design will meet his or her needs. Alignment agreement: | Models (e.g., physical, mathematical, computer models) can be used to simulate systems and interactions—including energy, matter, and information flows—within and between systems at different scales. Alignment agreement: |
Common Core State Standards - Math
-
(+) Use matrices to represent and manipulate data, e.g., to represent payoffs or incidence relationships in a network.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Telemedicine reflects the convergence of technological advances in a number of fields, including medicine, telecommunications, virtual presence, computer engineering, informatics, artificial intelligence, robotics, materials science, and perceptual psychology.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use various approaches to communicate processes and procedures for using, maintaining, and assessing technological products and systems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
National Council of Teachers of Mathematics - Math
-
create and use representations to organize, record, and communicate mathematical ideas
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
-
use representations to model and interpret physical, social, and mathematical phenomena
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
National Science Education Standards - Science
-
Use technology and mathematics to improve investigations and communications. A variety of technologies, such as hand tools, measuring instruments, and calculators, should be an integral component of scientific investigations. The use of computers for the collection, analysis, and display of data is also a part of this standard. Mathematics plays an essential role in all aspects of an inquiry. For example, measurement is used for posing questions, formulas are used for developing explanations, and charts and graphs are used for communicating results.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Scientists rely on technology to enhance the gathering and manipulation of data. New techniques and tools provide new evidence to guide inquiry and new methods to gather data, thereby contributing to the advance of science. The accuracy and precision of the data, and therefore the quality of the exploration, depends on the technology used.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Scientists conduct investigations for a wide variety of reasons. For example, they may wish to discover new aspects of the natural world, explain recently observed phenomena, or test the conclusions of prior investigations or the predictions of current theories.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Mathematics is essential in scientific inquiry. Mathematical tools and models guide and improve the posing of questions, gathering data, constructing explanations and communicating results.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Nebraska - Science
-
Use tools and technology to make detailed qualitative and quantitative observations
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Analyze and interpret data, synthesize ideas, formulate and evaluate models, and clarify concepts and explanations
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- computer with Internet access and Java installed and appropriate editing software (Eclipse, NetBeans, Java_Editor, JCreator, Jedi, etc.)
- (optional) Android device with Bluetooth discovery application
- DFS and BFS Algorithms Instructions
- Bluetooth Analysis Project - Part 1: Project Setup
- Bluetooth Analysis Project - Part 2: Graph Analysis
- Bluetooth Analysis Project - Part 3: Class Files
- Java zip files for data collection and analysis (to be installed and used for the analysis using an appropriate editing software): Graphing the Spread of Disease Java and Graphing the Spread of Disease Java Jung
- graph paper or Microsoft Excel, to graph collected data
- Data Collection Tables
- Lab Report Checklist
- Graphing the Spread of Disease Assessment, one per student
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/uno_connection_lesson01_activity1] to print or download.Pre-Req Knowledge
Knowledge of the Java programming language is required.
The teacher and students should have knowledge of graph theory including the following vocabulary terms: vertex, edge, adjacency list, adjacency matrix, depth first search (DFS) and breadth first search (BFS). For students, this knowledge can be gained in the associated lesson Making the Connection.
Introduction/Motivation
Graph theory is used by engineers in many different disciplines. Biomedical engineers use a process that is similar to what you will do in today's activity to simulate disease transmission. Graph theory can be used to represent the current state of the disease and help predict future spread of the disease. It is a very easy way to visually show the relationships present in a data set. Communication networks can be represented using graph theory as well as social networks like Facebook. Electrical and computer engineers use graph theory to show the relationships between components when designing new computer hardware like CPUs.
In this activity, you will explore the transmission of disease through a simulation. In our real-life simulation, you will determine who gets infected by the disease based on an individual's proximity to other people, who are infected, and by analyzing the data using graph theory concepts. Once the initial simulation is complete the students will develop possible solutions to preventing the spread of disease by changing the location of those who spread the infection.
The simulation will be ran again with the new location of the students. The students will analyze the data and reflect about the outcome of their second simulation.
Procedure
Background
This activity explores the application of graph theory, which is a visual representation for relationships present in a data set. In the activity, students model the collection of data related to how a disease is transmitted by collecting data on their proximity to others, based on the assumption that close proximity to an infected individual causes the disease to spread. The simulation activity is engaging because it uses a real-world application that affects all of us.
The data collection for this activity must be done before any analysis can be conducted. The method of data collection depends on whether or not Bluetooth devices are available; if not, data is collected manually. Both methods are outlined in detail in the Procedure section.
It is assumed that if you are reading and planning to use this activity that you are familiar with Java and Java editors since Java tools (such as the Java classes provided in the Attachments section) are the primary data analysis method of the activity. Complete step-by-step instructions are included in the attachments, which the teacher can use to learn the material as well as instruct students. If desired, print them out as student instruction sheets. So, if conducting with Bluetooth devices, the following documents provide the activity instructions: Part 1: Project Setup, Part 2: Graph Analysis, and Part 3: Class Files. The Java files for data collection and analysis are Graphing the Spread of Disease Java (zip), and Graphing the Spread of Disease Java Jung (zip). In addition, see examples from conducting the activity with students in Example Data and Graphs.
Before the Activity
- Review and familiarize yourself with all the instructions provided in the attachments.
- Decide if you are going to conduct multiple simulations (numerous trials) and if so, what they are. For example, multiple simulations could be performed to produce different datasets for each student. Or multiple simulations could mean that you re-conduct the proximity data collection experiment or set different condition for "infection" (such as 2/3 contacts result in infection, 1/3 contacts result in infection, etc.). Each simulation requires that students fill in separate data tables.
- Discuss possible ways to limit the spread of infection based on the inputs to run the simulation.
- Gather materials and make paper and digital copies of the necessary handouts and files.
- You need only make copies of one of the tables in the Data Collection Tables, depending on how the data is being collected. Also, make enough copies so students have a new table for each planned simulation/trial, if conducting more than one.
- Prepare for the students all the computers and attachments with instructions and Java files.
With the Students—Data Collection
After presenting the Introduction/Motivation content, hand out the data collection worksheets and have students collect data on their proximity to others, either by Bluetooth Android device or manually, following the pertinent steps below.
If Bluetooth Android devices are the collection method, have students use Bluetooth discovery to collect the data in the classroom with all students following these steps.
- As you recall, we are collecting data that will be used to simulate disease transmission.
- You are considered in close enough contact (proximity) to transmit the disease (with Bluetooth, this could mean everyone within 10 meters) when your Bluetooth devices discover other Bluetooth devices. Only Bluetooth devices participating in the simulation are considered.
- Direct students to make their Bluetooth either "discoverable" or "not discoverable" and then every so often change their status randomly. This means that at any given time some devices are on (discoverable) while others are off (not discoverable). The device recognitions found via Bluetooth count as disease transmissions and need to be recorded.
- Let's set a data collection time period of three minutes. (Make this three to five minutes or longer, as determined by the teacher.)
- The Bluetooth detections must be noted so that the transmissions can be counted. So when another Bluetooth device is discovered, you must record in your data collection table (see Figure 1) all data related to that contact, including:
- which simulation is being conducted, if different trials are going to be conducted, for instance, to run simulations with different infection rates (contact only provides infection 2/3 times, etc.)
- UserID: the device name of the person recording data
- close proximity to UserID: the device name of who you came in contact with
- time of infection: The time of infection column is used to identify when the other data in the same line of the table was recorded, which is important because diseases have incubation periods and take time to run their course. Knowing the time of infection is critical to understanding the duration and onset of the disease. The UserID and time of infection will be used to sort the data when students combine all their data into one table.

Figure 1. Data collection table for use with Bluetooth devices.
- Then have students collect data on their interactions within the course of their normal activities. They can freely move around the classroom during the collection period and do as they wish, as long as they follow any classroom rules and make sure to collect data as specified (described below). If some students want to remain at their desks, that is fine as well. Only those who are in close proximity to each other are exposed to the disease, so students sitting at desks away from others represent being isolated in remote areas where the disease is less likely to be transmitted.
- Then the teacher should run additional simulations in order to collect different data sets, simply end the simulation, ask students to change or not change their Bluetooth status.
- Before beginning the next simulation, get feedback from the students about how to limit the spread of the infection. Then begin the simulation again for another three minutes.
If Bluetooth Android devices are not available, have students collect proximity data manually within the classroom, following these steps.
- As you recall, we are collecting data that will be used to simulate disease transmission.
- First, let's set a proximity estimate, such as being within arm's length. That means that you are considered in close enough contact (proximity) to transmit the disease when you are within arm's length of another person.
- Then, let's set a data collection time period of five minutes. (Make this three to five minutes or longer, as determined by the teacher.)
- Every time you come in contact with another person, you must record it as a contact in your data collection table (see Figure 2). For each contact, record the following data:
- which simulation is being conducted, if different trials are going to be conducted (for instance, to run simulations with different infection rates [contact only provides infection 2/3 times, etc.])
- name of the person recording data
- name of the person who you came in contact with
- time of infection: The time of infection column is used to identify when the other data in the same line of the table was recorded, which is important because diseases have incubation periods and take time to run their course. Knowing the time of infection is critical to understanding the duration and onset of the disease. The name of the recorder and time of infection will be used to sort the data when students combine all their data into one table.

Figure 2. Data collection table for manual collection.
- Then have students collect data on their interactions within the course of their normal activities. They can freely move around the classroom during the collection period and do as they wish, as long as they follow any classroom rules and make sure to collect data as specified (described below). If some students want to remain at their desks, that is fine as well. Only those who are in close proximity to each other are exposed to the disease, so students sitting at desks away from others represent being isolated in remote areas where the disease is less likely to be transmitted.
- The teacher should run additional simulations (trials) in order to collect different data sets.
- Before the next trial, discuss ways to limit the spread of the infection. Then talk about the pros and cons of implementing their suggestions in the real world. Repeat the simulation process again for another five minutes, filling in new data tables.
With the Students—Data Analysis
- After collecting data (and depending on the data collected in the simulation), a number of questions could be answered through analysis of the data, such as:
- Which students are connected through close proximity to all other students?
- Given an initial infected individual, which students are infected?
- How could the spread of infection be minimized?
- After some class analysis of the data, have student groups create graphs of nodes and edges representing their disease transmission simulations (see Figure 3).
- Provide groups with the lab report checklist, assigning them to each create lab write-ups of the simulation that include the following components: procedure, data in table format, drawn graphs, data analysis, calculations (vertex list, edge list, adjacency matrix, adjacency list, DFS search, and BFS search) and conclusions.
- Conclude by administering summative assessment graph theory problems, as described in the Assessment section.
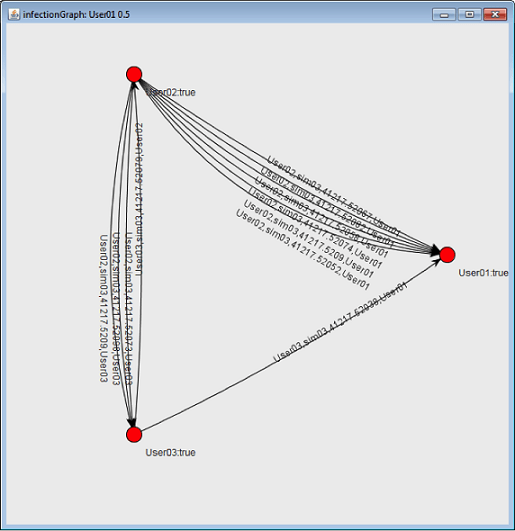
Figure 3. An example disease transmission simulation graph using data collected via Bluetooth on mobile devices.
Vocabulary/Definitions
adjacency list: An adjacency list for a graph has a row for each vertex and contains the vertex label followed by the vertex labels of adjacent vertices.
adjacency matrix: An adjacency matrix for a graph with n vertices is an n x n matrix where each entry (i, j) is a 1 if there is an edge in the graph between vertex i and j; otherwise the entry is 0.
breadth first search (BFS): An algorithm or method of graph traversal that considers a given node as the parent and connected nodes as children; BFS visits the sibling vertices before the child vertices.
child vertex: Nodes in a graph that are directly connected to the current node. If the first node (parent node) is selected, then one of the nodes connected to it is the child node. That child node then becomes a parent node, and a node connected to it becomes a child node.
depth first search (DFS): An algorithm or method of graph traversal that considers a given node as the parent and connected nodes as children; DFS visits the child vertices before visiting sibling vertices.
edge (edge graph): A connection between nodes.
graph theory: The study of mathematical structures (graphs) so as to model relationships between objects from a collection.
sibling vertex: Nodes in a graph that are on the same level as the child node, connected to the same parent node with a single edge. Sibling nodes may or may not be connected to each other.
six degrees of separation: The theory that everyone is six or fewer steps away from knowing any other person in the world. This theory implies that a chain of "friend to friend" can be made to connect any two people in the world in a maximum of six steps.
vertex list: A listing of all the vertices present in a graph.
vertex or node: The fundamental unit of which graphs are formed. Plural: vertices.
Assessment
Opening Questions: Review and confirm students' understanding of key pre-requisite concepts by asking the following questions:
- In the context of graph theory, what is an edge? (Answer: An edge is a connection between two vertices showing a relationship.)
- What are vertices? (Answer: Vertices are the points in the graph representing what is being analyzed. In a social network or disease transmission application, vertices are people. In a network, the vertices are computers and devices.)
- How can graph theory be applied to engineering? (Answer: Graph theory can be applied any time a visual representation of the relationships between objects is desired. For example, engineers use graph theory in computer networks [computer engineers], social networks and computer programming [software engineers], the arrangement and design of computer hardware [electrical and computer engineers].)
- How can the information obtained from graph theory lead to a solution to preventing the spread of disease? (Answer: By running computer simulations we can see which people may be infected the quickest. Knowing this enables emergency responders to know where to focus their efforts to prevent further spread of the infection.
Formative Assessment: While students are engaged in the activity, observe and verify these (or similar) assessment queries:
- Are students able to realize and record how the disease is being transmitted between people?
- Are students able to create graphs representing the data collected in the simulation?
- Do students understand the concepts of vertex, edge, depth first search and breadth first search?
Summary Lab Report: At activity end, have students each complete and turn in lab reports summarizing the activity, using the Lab Report Checklist to inform their report requirements. Use the same checklist as a grading rubric. Review their reports to assess their level of comprehension of the concepts.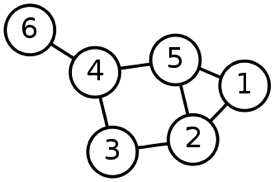
Summative Assessment: Have students complete the five problems provided on the Graphing the Spread of Disease Assessment (as well as below) to gauge their understanding of graph theory. Answers are provided on the Graphing the Spread of Disease Assessment Answer Key.
Given the Figure 4 graph, answer the following questions:
- What is the vertex list for this graph?
- What is the edge list for this graph?
- What is the adjacency matrix for this graph?
- What is the adjacency list for this graph?
- Starting at vertex 1 and using a DFS search, what would be the visitation order of the vertices? Do the same for a BFS search.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn and apply concepts and methods of graph theory to analyze data for different relationships such as friendships and physical proximity. They are asked about relationships between people and how those relationships can be illustrated.

Students learn about complex networks and how to represent them using graphs. They also learn that graph theory is a useful mathematical tool for studying complex networks in diverse applications of science and engineering, such as neural networks in the brain, biochemical reaction networks in cells...

Students use graph theory to create social graphs for their own social networks and apply what learn to create a graph representing the social dynamics found in a dramatic text.

Building on their understanding of graphs, students are introduced to random processes on networks. They walk through an illustrative example to see how a random process can be used to represent the spread of an infectious disease, such as the flu, on a social network of students.
Copyright
© 2013 by Regents of the University of Colorado; original © 2013 Board of Regents, University of NebraskaContributors
Steve Hamersky, Brian SandallSupporting Program
IMPART RET Program, College of Information Science & Technology, University of Nebraska-OmahaAcknowledgements
The contents of this digital library curriculum were developed as a part of the RET in Engineering and Computer Science Site on Infusing Mobile Platform Applied Research into Teaching (IMPART) Program at the University of Nebraska-Omaha under National Science Foundation RET grant number CNS 1201136. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: August 22, 2018






User Comments & Tips