Hands-on Activity Statistical Analysis of Methods to Repair Cracked Steel

Learning Objectives

After this activity, students should be able to:

• Use box-and-whisker plots to analyze various data sets.
• Use bar graphs to compare and make conclusions about multiple data sets.
• Use technology to efficiently perform statistical analyses and graph data.
• Use PowerPoint® to present results and conclusions.
• Describe the statistical analyses performed on experimental data.
• Clearly state final conclusions resulting from statistical analyses.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

NGSS: Next Generation Science Standards - Science

Common Core State Standards - Math

State Standards

Materials List

Each student needs:

• graphing calculator (TI-Nspire™ recommended)*
• USB 2.0 high-speed A to mini-B cable*
• TI-Nspire™ Computer Link Software; for Windows (exe) or Macintosh (dmb); download here 
• PC computer loaded with Microsoft® Excel® and PowerPoint® software
• Pre-Activity Test, one per person
• Project Guidelines and Rubrics, one per person
• Experimental Data Sets (PDF or Word® file), one per person
• Experimental Data Sets (Excel® file), one per student (only for students if using the TI-Nspire™ CX Student Software)

*An optional alternative to the graphing calculator and USB connector cable is to use a computer with the TI-Nspire™ CX Student Software.

To share with the entire class:

• (optional) projector and computer/laptop to display to the class the Activity Intro Presentation (a PowerPoint® file) and Experimental Data Set (an Excel® file) during the activity introduction
• (optional) the hardware and software tools to create videos (instead of final slide presentations)

Worksheets and Attachments

Pre-Req Knowledge

This activity is designed for students taking AP Statistics. Students should be familiar with:

• Central tendency measurements, including mean, median and mode
• Five-number summary
• Standard deviation and coefficient of variation
• Box-and-whisker plots, simple and clustered bar graphs, and Pareto charts

Students should also have basic computer skills and be familiar with Microsoft® Excel® and PowerPoint®, and graphing calculators.

Teach students the associated lesson to help them understand the context of the data to be analyzed.

Introduction/Motivation

Rehabilitation of cracked steel structures is an important and challenging task. Improving the resiliency, extending the life, and maintaining the integrity of civil infrastructure is a necessary priority for governments around the globe because structural failures can have fatal consequences. In the associated lesson, we learned about the collapse of the Minneapolis I-35W Bridge over the Mississippi River and the Norwegian North Sea Alexander Kielland platform—both human disasters that are examples of the life-protecting professional responsibility of civil engineers to design and maintain safe structures.

Visualize yourselves as civil engineers working for our city’s Department of Public Works and Engineering. Your responsibility is the operation, maintenance, construction management, and technical engineering of the city's public infrastructure. One of your duties is the periodic inspection of the city’s steel support structures and their corresponding repair as soon as any fracture or cracking is detected.

Because of your expertise, you are invited to participate in a meeting with the mayor and city council. One discussion point is the new budget for repair of the city’s civil infrastructure. One council member expressed concern about the cost and effectiveness of the traditional repair methods used by the city. The council member is concerned that the current methods that require modification of the original structure, such as drilling holes, may compromise the structures’ reliability over time. The city council and mayor have asked you to find a new or different repair method that does not alter the original structures.

So that you are data-driven in your recommendations, you decide to conduct an analysis of repair methods developed in seven civil engineering research centers around the world: University of Massachusetts (USA), Southwest Jaiton University (China), National Technical University of Athens (Greece), Technical University of Denmark, Monash University (Australia), ABC Politecnico di Milano (Italy), and the University of Houston (USA). Based on the findings from your statistical analysis, you will select the most efficient method and then present your results, evidence-based conclusions and recommendation to the mayor and city council.

Procedure

Background

In this activity, students’ engineering challenge is to analyze 12 data sets of experimental results from seven research centers to determine the best patching method to rehabilitate steel structures. To help them make sense of the data, first teach the associated lesson to give them a basic and broad understanding of composites, fiber-reinforced polymers, carbon fiber, epoxy adhesives, nitinol, and repair patches. The activity data analysis requires students to determine for each data set: mean (mean fatigue life), standard deviation, coefficient of variation, trimmed mean, the five-number summary and the associated box-and-whisker plot. Students must also compute the relative efficiency and relative median efficiency (reported as percentages) of each patching method. The relative efficiency E_R is defined as:

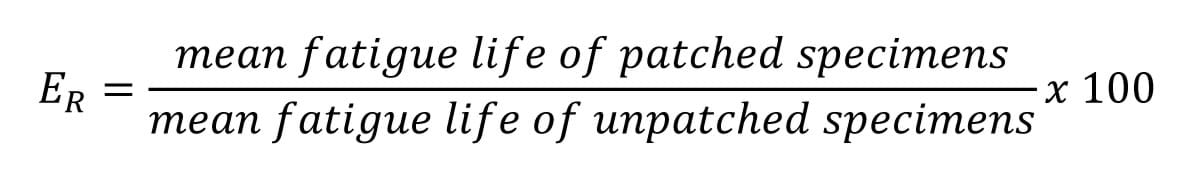
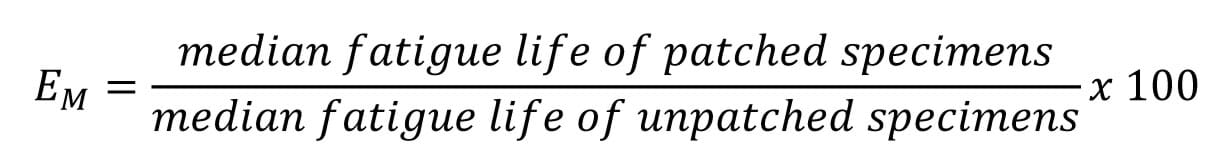
Suggested Activity Schedule

The estimated time to perform this data analysis activity is six 50-minute sessions for a three-member team “working-in-parallel.” (Larger teams “working-in-parallel” can reduced this time; a four-member team may work four data sets per day, and finish the data analysis in four days). The suggested work flow:

Day 1: (50 minutes)

• University of Massachusetts. Data Sets 1 and 2
• Southwest Jiaotong University. Data Set 3

Day 2: (50 minutes)

• Southwest Jiaotong University. Data Set 4
• National Technical University of Athens. Data Set 5
• Technical University of Denmark. Data Set 6

Day 3: (50 minutes)

• Technical University of Denmark. Data Set 7
• Monash University. Data Sets 8 and 9

Day 4: (50 minutes)

• ABC Politecnico di Milano. Data Sets 10 and 11
• University of Houston. Data Set 12

Day 5: Relative efficiencies analysis; bar graph and Pareto chart (50 minutes)

Day 6: Group presentations (estimated 50 minutes; time may vary, depending on class size and presentation expectations)

Before the Activity

• Gather materials and make copies of the Pre-Activity Test, Project Guidelines and Rubrics, and Experimental Data Sets. Each student needs a graphing calculator, cable, hardcopy of the data sets, and computer OR computer, software and Excel® data file, so that students can simultaneously crunch numbers as a group.
• Alternative setup: If the TI-Nspire™ CX Student Software is available on the student computers, it can be used for all computations and graphs instead the handheld calculators, thereby avoiding the necessity to transfer files between the calculators and PCs. In this case:
• Make sure that you are familiar with the TI-Nspire™ CX Student Software.
• Transfer the Experimental Data Sets (the Excel^® file) to the student computers.
• Prepare computers for each student, with Excel^®, PowerPoint^® and TI-Nspire™ Computer Link Software installed, so that teams are able to work in parallel.
• So that you are prepared to model the steps for students (if needed), it is recommended that teachers perform (at least some of) the computations, data analysis, graphs, connectivity, and file transfers with the TI-Nspire™ Computer Link Software that students will be required to do.
• (optional) Prepare an example data set (somewhat like the 12 data sets) to use during the procedure (step 7, below) to explain and demonstrate (if needed) what students need to do for each of the 12 data sets.
• (optional) Prepare to display to the entire class the Activity Intro Presentation (a PowerPoint^® file) and the Experimental Data Sets (the Excel® file). Note: The slides are “animated,” so run the file as a slide show and click to bring up the next item.

With the Students

1. Administer the pre-activity test. Check students’ answers to verify their understanding of the foundational statistical analysis concepts necessary to succeed in the activity.
2. Present to the class the Introduction/Motivation section content, which introduces the hypothetical engineering challenge—a real-world applied use for statistical analysis. (optional) Use the nine-slide presentation to provide visuals for the class as you introduce the activity components in more detail. Topics covered: the engineering challenge, information on data analysis, graphing and fatigue life ratio, and final presentation main components.
3. Pass out the guidelines/rubrics handout, which describes the engineering challenge and provides project guidelines in an overview format to guide students through the entire project.
4. Let students set up work teams of three members each. Advise students that in order to finish the analysis of all the data sets in the allotted time each day (3 sets in 50 minutes), they need to “work in parallel,” that is, have each group member simultaneously perform one analysis.
5. Explain to the student teams that:

• Their task is to analyze 12 different data sets coming from seven different research centers.
• The data consists of the results of CFRP patched and unpatched cracked steel specimens, tested under the same stress conditions.
• Every research center set up different experimental conditions.
• Every record in each data set is the maximum number of times the tested patched or unpatched specimens resisted the constant and periodic stress applied, that is, the number of times (cycles) the stress was applied before the specimens broke.

6. Project the data sets spreadsheet and flip through the different tabs to show the class how it is organized. Explain that the number of records in each column is the number of specimens tested.
7. Using one of the data sets (or a similar example data set created you created in advance) explain (or demonstrate, if needed) what students need to do for each of the 12 data sets:

A.    Compute mean and standard deviation. The means represent the mean fatigue life for the patched and unpatched tested sets, and the standard deviations are the average spread of the individual fatigue lives around their mean values. The standard deviation gives a first measurement for the variability of the effectiveness of the patching method.

B.    Calculate coefficient of variation. This compares the variability of the effectiveness of the patching method with the extended fatigue life achieved by the patched specimens.

C.    Find the five-number summary. These numbers quantify the overall variability or range of the results, provide the median fatigue life of the specimens, the symmetric or non-symmetric distribution of the data, and display any anomalous performance values or outliers that could be discarded in the final analysis.

D.    10% trimmed mean. This gives an alternative value for the mean fatigue life, computed after the largest and/or smallest anomalous test results are discarded. For data sets with large and/or small outliers, this alternative average could give a more representative mean fatigue life value.

E.     Relative efficiencies. These values measure the extended mean fatigue life and extended median fatigue life of the patched versus unpatched specimens (E_R and E_M, respectively). The values represent the number of times the patching repair method extended the mean and median fatigue lives of cracked specimens.

F.     Box-and-whisker plots. For every one of the 12 data sets, display the graph of five-number summaries obtained for the patched and unpatched records in the same graphing window. This can be easily done using graphing calculator capabilities. In every one of the 12 generated graphs, require students to also include a line representing the mean fatigue life of the patched and unpatched specimens.

G.   Statistics and graphs analysis. To conclude, do a brief and concise analysis of all the previous information and of the box-and-whisker plots obtained, as well your conclusion as to the effectiveness of the repair used.

8. Have students display their results from the A-G analysis in a table format in Word® or Excel®, which makes it convenient to incorporate it in their final results presentations. Suggest (or require) that students use a format like that used one in the Experimental Data Analysis Answer Key.
9. If using graphing calculators, inform students that all of the required data analyses can be performed using the graphing calculators. Explain that they will need to manually load the data sets into the calculators, and since few values need to be typed in, it can be done quickly. Remind students to double-check that they have typed in the data correctly. If the TI-Nspire™ CX Student Software is available, copy/paste the data from the Excel® data sets file, and perform all the above calculations using this software on the PCs, avoiding the file transfer process.
10. Have students transfer the box-and-whisker plots from their calculators to the PCs using the TI-Nspire™ Computer Link Software and the USB cable. Remind students to include these graphs in their results presentations.
11. Once all the above tasks are done, direct groups to each create an Excel® table with the relative efficiencies (E_R and E_M) obtained for each of the 12 data sets that specifies the research center the efficiencies came from (see the Relative Efficiencies Analysis section starting on page 17 of the Experimental Data Analysis Answer Key). This table provides the necessary information to create (using Excel®) a relative efficiencies clustered bar graph and its associated Pareto chart for E_R, which are graphs that help to visually determine the most efficient patching repair method.
12. Tell students that once they have completed the data analyses, it is time to create reports and presentations of their results. Use the rubric to outline expectations that work with the class time available to devote to group presentations. Require reports to include: project background, data analyzed, obtained results and related graphs, and the corresponding statistical analysis and conclusions; refer students to the rubric for details.

Vocabulary/Definitions

bar graph: A graphical display of grouped statistical data presented in the form of rectangular bars. The independent variable values are discrete, while the dependent variable values (indicated by rectangle length) may be discrete or continuous. Also called a bar chart.

box-and-whisker plot: A graphical display of the five-number summary.

coefficient of variation: The ratio of the standard deviation to the mean, multiplied times 100 and reported as a percentage.

five-number summary: A descriptive statistic that includes 1) the minimum value, 2) the lower or first quartile, 3) the median or second quartile (middle value), 4) the upper or third quartile, and 5) the maximum value.

interquartile range: A measure of variability. The difference between the third and first quartiles.

mean: The average of a set of numbers; the sum of the numbers, divided by the total count of numbers.

median: The “middle” number from a sorted list of numbers.

percentile: A defined value such that a percentage (X%) of the data fall at or below it, and (100-X%) of the data fall at or above it.

quartile: The percentile that divides a data set into four equal groups (quarters).

range (statistics): The difference between the highest and lowest values in a data set.

standard deviation: A measure of how spread out a set of numbers is around its mean.

trimmed mean: An averaging method that reduces the effects of statistical outliers; the mean of the values left after removing a specified percentage (usually 5% or 10%) of the smallest and largest data. Also called truncated mean.

Assessment

Pre-Activity Assessment

Pre-Activity Skills Test: Before starting the activity, administer the Pre-Activity Test to verify that students know how to obtain central tendency measurements, five-number summaries, box-and-whisker plots, clustered bar graphs, and Pareto charts.

Activity Embedded Assessment

Partial Data Graphing and Analysis: As students generate box-and-whisker plots for each of the data sets, oversee their progress and assist as needed.

Analysis Summary File: Require each team to prepare an Excel® file containing tables with its analyzed data and generated statistics. Expect an “outstanding” summary file to include the associated box-and-whisker plots and text boxes that outline the statistical analyses and conclusions. Refer to the Experimental Data Analysis Answer Key.

Post-Activity Assessment

Project Results Presentations: Direct teams to create final reports using PowerPoint® (or videos, if that capability is available). Require the reports to include components such as project background, data analyzed, obtained results and related graphs, and corresponding statistical analyses and conclusions, as detailed in the Project Guidelines and Rubrics. For non-standalone slide shows, students make in-person presentations of their results. Give teams each 10 minutes to make the presentation plus a few extra minutes for Q&A. Use the rubric to grade students’ reports and presentations and assess their comprehension and competence in this statistical analysis project. See the Experimental Data Analysis Answer Key for expected results.

Troubleshooting Tips

Because of the background information necessary to help students make sense of the data to be analyzed, it is important to use the resources in the associated lesson. For some statistical analysis, graphing and results presentations support, you are welcome to request assistance from the author, Miguel R. Ramirez, at mramirez2@galenaparkisd.com.

Activity Scaling

For lower grades, use the data in either a practice or activity format to teach middle school students to obtain means, five-number summaries, and to produce box-and-whisker plots by hand or using graphing calculators. Limit the results presentation to a manual sketch of the graphs or, if the resources are available (computers with PowerPoint® and TI-Nspire™ CX Student Software), a slide show with the captured computer-generated graphs.

Additional Multimedia Support

Show students a photograph of the collapsed Alexander Kielland drilling platform structure, at the Norwegian Oil and Gas Association’s Norway’s Petroleum History web page at https://www.regjeringen.no/en/topics/energy/oil-and-gas/norways-oil-history-in-5-minutes/id440538/.

The following AP Statistics tutorials created by the author may be helpful. They include short videos (4 to 17 minutes), quizzes and notetaking guides.

• Measurements of Central Tendency: https://www.sophia.org/tutorials/ap-statistics-ch-311-measures-of-central-tendency?playlist=03-averages-and-variation
• Measurement of Variation: Standard Deviation: https://www.sophia.org/tutorials/ap-statistics-ch-322-measures-of-variation-standar?playlist=03-averages-and-variation
• Coefficient of Variation: https://www.sophia.org/tutorials/ap-statistics-ch-323-cofficient-of-variation?playlist=03-averages-and-variation
• Percentiles and Quartiles: https://www.sophia.org/tutorials/ap-statistics-ch-341-percentiles-and-quartiles?playlist=03-averages-and-variation
• Box-and-Whisker Plots: https://www.sophia.org/tutorials/ap-statistics-ch-342-box-and-whisker-plots?playlist=03-averages-and-variation
• Bar Graphs: https://www.sophia.org/tutorials/ap-statistics-ch-211-bar-graphs?playlist=02-organizing-data
• Pareto Charts: https://www.sophia.org/tutorials/ap-statistics-ch-212-pareto-charts?playlist=02-organizing-data

Ti-Nspire™ CAS CX Box-and-Whiskers List Spreadsheets and More Screen Captures (5:22 minutes): https://www.youtube.com/watch?v=2RGqA-fokjU

Texas Instruments Education Technology Resources:

• TI-Nspire Computer Link Software for Windows (EXE) and Macintosh (DMB); download here.
• Features Summary for TI-Nspire Computer Link Software at https://education.ti.com/en/us/products/computer_software/connectivity-software/ti-nspire-computer-link-software/features/features-summary
• Features Summary for Standard A to Mini-B USB Connectivity Cable at https://education.ti.com/en/us/products/computer_software/connectivity-software/standard-a-to-mini-b-usb-connectivity-cable/features/features-summary
• TI-Nspire CX / TI-Nspire CX CAS Student Software Guidebook, v 4.2; view online or download PDF at https://education.ti.com/en/us/guidebook/details/en/15E1291AC8CA4EF8A081110D38EB2849/ti-nspirecxstudentsoftwareguidebook
• Using the TI-Nspire Computer Link Software Guidebook; download PDF at https://education.ti.com/en/us/software/details/en/82035809F7E6474099944056CCB01C20/ti-nspire_computerlink
• TI-Nspire CX Handheld: https://education.ti.com/en/us/products/calculators/graphing-calculators/ti-nspire-cx-handheld/tabs/overview

References

Other Related Information

AP Statistics topics and timing note: This activity and its associated lesson are intended to be taught during the last six weeks of the school year to address topics covered in the AP Statistics course, including central tendency measurements and five-numbers summary. The total time required for the lesson and activity is nine 50-minute sessions. Use the project results presentation grades that students obtain in the associated activity as part of their first semester final test grades.

Copyright

Contributors

Supporting Program

Acknowledgements

This digital library content was developed by the University of Houston's College of Engineering under National Science Foundation GK-12 grant number DGE 0840889. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.

The author also thanks Fritz Claydon; RET program director, Stuart Long and Debora Rodrigues, RET academic advisors; Mila Taylor, Marjorie Hernandez and Andrea Lee, RET advisors; as well as the National Science Foundation for its funding of the RET program.