Quick Look
Grade Level: 11 (9-12)
Time Required: 45 minutes
Lesson Dependency:
Subject Areas: Algebra
Summary
Students revisit the mathematics required to find bone mineral density, to which they were introduced in lesson 2 of this unit. They learn the equation to find intensity, Beer's law, and how to use it. Then they use the associated activity to investigate real world applications prior to completing a sheet of practice problems that use the Beer's law equation.Engineering Connection
Students see the real-world connection with this material right away. Beer's law and the other equations that they learn in this lesson are mathematical tools that biomedical engineers use every day when they make bone mineral density readings. Environmental engineers also use light intensity measurements when designing solar panels and other forms of energy storage. Almost every type of engineer knows and uses Beer's law.
Learning Objectives
After this lesson, student should be able to:
- Apply their knowledge of logarithms to solve Beer's law problems.
- Explain the breath of the applications of logarithms.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Interpret expressions that represent a quantity in terms of its context
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Interpret parts of an expression, such as terms, factors, and coefficients.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve simple rational and radical equations in one variable, and give examples showing how extraneous solutions may arise.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
(+) Understand the inverse relationship between exponents and logarithms and use this relationship to solve problems involving logarithms and exponents.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
For exponential models, express as a logarithm the solution to abct = d where a, c, and d are numbers and the base b is 2, 10, or e; evaluate the logarithm using technology.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use the properties of exponents to transform expressions for exponential functions.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Analyze how technology transfer occurs when a user applies an existing innovation developed for one function to a different purpose.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Tennessee - Math
-
(+) Understand the inverse relationship between exponents and logarithms and use this relationship to solve problems involving logarithms and exponents.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/van_bmd_less4] to print or download.Introduction/Motivation
Recall from lesson 1 that you are working for a company that makes small specimen cabinet x-ray machines for medical research. Today you will learn how to do some calculations with the data that you might collect from such a machine.
Lesson Background and Concepts for Teachers
Calculation of Bone Mineral Density:
The basic equations for dual-photon absorptiometry can be derived from a number of underlying assumptions. First, it is assumed that the material is composed of varying amounts of only two substances (in this case bone and soft tissue). Second, it is assumed that scatter can be ignored. Under these circumstances, for any given photon energy, the number of photons striking the detector (N) can be calculated from the number of incident photons (No) using Beer's law.
Beer's law: 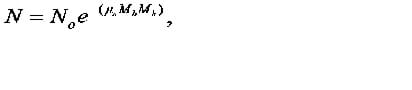
where μs and μb represent the mass attenuation coefficients (cm2/g) of soft tissue and bone (respectively) and Ms and Mb represent the area densities (g/cm2) of the two tissue types.
I = I o e -μl
I = Intensity.
I0 = Intensity with no object.
μ = attenuation coefficient (depends upon material and x-ray energy).
l = length of the x-ray path.
Lecture Information
Present to students the BMD Math Presentation, a PowerPoint® file. Then have students complete the BMD Math Practice Problems. Administer the Log Quiz 2. Then students are ready to conduct the associated activity, Light Intensity Lab.
To answer the Challenge Question introduced in lesson 1, students next must Go Public. Refer to the Pamphlet Poster Paper Instructions for how students are to present all that they have learned about logarithms and bone mineral density during the course of the entire unit.
Associated Activities
- Light Intensity Lab - In this lab exercise, students learn how to measure light intensity through transparencies.
Assessment
Post-Introduction Assessment
Practice Problems: At lesson end or as homework, assign students to complete the BMD Math Practice Problems. Review their answers to assess the depth of their understanding.
Lesson Summary Assessment
Quiz: At lesson end, administer the 13-question, multiple-choice Log Quiz 2, which covers all types of logarithmic problems covered in this unit. Review students' answers to gauge their comprehension.
Student Presentations: In order to answer the unit challenge question first posed in lesson 1, have students create posters, pamphlest or papers, as described in the Pamphlet Poster Paper Instructions.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn about the science and math that explain light behavior, which engineers have exploited to create sunglasses. They examine tinted and polarized lenses, learn about light polarization, transmission, reflection, intensity, attenuation, and how different mediums reduce the intensities of ...

Students continue an examination of logarithms in the Research and Revise stage by studying two types of logarithms—common logarithms and natural logarithm. They take notes about the two special types of logarithms, why they are useful, and how to convert to these forms by using the change of base f...

Students examine the definition, history and relationship to exponents; they rewrite exponents as logarithms and vice versa, evaluating expressions, solving for a missing piece. Students then study the properties of logarithms (multiplication/addition, division/subtraction, exponents).

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...
Copyright
© 2013 by Regents of the University of Colorado; original © 2006 Vanderbilt UniversityContributors
Kristyn Shaffer; Megan JohnstonSupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: May 23, 2019







User Comments & Tips