Quick Look
Grade Level: 11 (9-12)
Time Required: 1 hours 45 minutes
(can be split into two 50-minute sessions)
Lesson Dependency:
Subject Areas: Algebra
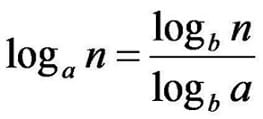
Summary
Students continue an examination of logarithms in the Research and Revise stage by studying two types of logarithms—common logarithms and natural logarithm. In this study, they take notes about the two special types of logarithms, why they are useful, and how to convert to these forms by using the change of base formula. Then students can solidify their understanding with the associated activity to see how these types of logarithms can be applied to solve exponential equations. They compute a set of practice problems and apply the skills learned in class.Engineering Connection
All types of engineers use natural and common logarithms.Chemical engineers use them to measure radioactive decay, and pH solutions, which are measured on a logarithmic scale. Exponential equations and logarithms are used to measure earthquakes and to predict how fast your bank account might grow. Biomedical engineers use them to measure cell decay and growth, and also to measure light intensity for bone mineral density measurements, the focus of this unit.
Learning Objectives
After this lesson, students should be able to:
- Define the number e.
- Define the common and natural logarithms.
- Use common and natural logarithms to evaluate expressions.
- Use the change of base formula to convert to a common or natural logarithm in order to evaluate expressions and solve equations.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
(+) Understand the inverse relationship between exponents and logarithms and use this relationship to solve problems involving logarithms and exponents.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
For exponential models, express as a logarithm the solution to abct = d where a, c, and d are numbers and the base b is 2, 10, or e; evaluate the logarithm using technology.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Analyze how technology transfer occurs when a user applies an existing innovation developed for one function to a different purpose.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/van_bmd_less3] to print or download.Introduction/Motivation
We are going to continue our study of logarithms today. Do you remember what we read a few days ago about the bone mineral density test and how we found out that we needed to know about logarithms in order to be able to read the bone mineral density image? Now that we have learned about the basics of logarithms—that they are the inverse of exponents, and some of their algebraic properties—let's move on to learn about the different types of logarithms.
You may have noticed that all the logarithms we have seen so far have a subscript number next to them. This is called the base. We have been working with other bases, usually small whole number, such as 2, 3 and 5. When no base is given, it is implied that the base is 10. These types of logarithms are called common logarithms. Today, we will compare the common logarithm to the natural logarithm, which instead of having a base of 10, has a base of e. Following this activity have students complete the Linear Regression of Bone Mineral Density Scanners activity to practice their gained knowledge by completing an exercise that shows logarithmic relationships byrelating the number of BMD scanners to time.
Lesson Background and Concepts for Teachers
Common Logarithms
- A common logarithm has a base of 10.
- If no base is given explicitly, it is common.
- You can easily find common logs of powers of 10.
- You can use your calculator to evaluate common logs.
Natural Logarithms
- Natural logarithms have a base of e.
- We write natural logarithms as ln.
- In other words, loge x = ln x.
- The mathematical constant e is the unique real number such that the derivative (the slope of the tangent line) of the function f(x) = ex is f '(x) = ex, and its value at the point x = 0, is exactly 1.
- The function ex so defined is called the exponential function.
- The inverse of the exponential function is the natural logarithm, or logarithm with base e.
- The number e is also commonly defined as the base of the natural logarithm (using an integral to define the latter), as the limit of a certain sequence, or as the sum of a certain series.
- The number e is one of the most important numbers in mathematics, alongside the additive and multiplicative identities 0 and 1, the constant π , and the imaginary number i.
- e is irrational, and as such its value cannot be given exactly as a finite or eventually repeating decimal. The numerical value of e truncated to 20 decimal places is: 2.71828 18284 59045 23536.
Associated Activities
- Linear Regression of Bone Mineral Density Scanners - Students complete an exercise showing logarithmic relationships and how to find the linear regression of data that does not seem linear upon initial examination. They relate the number of BMD scanners to time.
Assessment
Practice Problems: Assign students the practice problems. Grade their answers to assess the learning objectives.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to the technology of flexible circuits, some applications and the photolithography fabrication process. They are challenged to determine if the fabrication process results in a change in the circuit dimensions since, as circuits get smaller and smaller (nano-circuits), this c...
Copyright
© 2013 by Regents of the University of Colorado; original © 2006 Vanderbilt UniversityContributors
Kristyn Shaffer; Megan JohnstonSupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government..
Last modified: May 30, 2019






User Comments & Tips